Let \(\mathcal{T}\) be the triangular region with vertices \((1,0,0),(0,1,0)\), and \((0,0,1)\) oriented with upward-pointing normal vector (Figure 16). Assume distances are in meters.

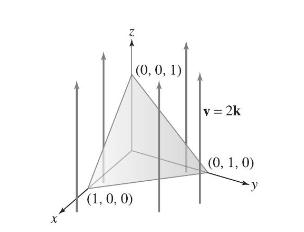
A fluid flows with constant velocity field \(\mathbf{v}=2 \mathbf{k}\) (meters per second). Calculate:
(a) the flow rate through \(\mathcal{T}\).
(b) the flow rate through the projection of \(\mathcal{T}\) onto the \(x y\)-plane [the triangle with vertices \((0,0,0),(1,0,0)\), and \((0,1,0)]\).

X (1,0,0) (0, 0, 1) v = 2k (0, 1, 0) -y