Let r(t) = (x(t), y(t), z(t)) be a path with curvature (t) and define the scaled path

Let r(t) = (x(t), y(t), z(t)) be a path with curvature κ(t) and define the scaled path r₁(t) = (λx(t), λy(t), λz(t)), where λ ≠ 0 is a constant. Prove that curvature varies inversely with the scale factor. That is, prove that the curvature κ₁(t) of r₁(t) is κ₁(t) = λ⁻¹κ(t). This explains why the curvature of a circle of radius R is proportional to 1/R (in fact, it is equal to 1/R). Use Eq. (3).

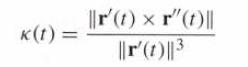
Transcribed Image Text:

k(t) = ||r'(1) r"(t)|| ||r' (t)||