Prove that if is positive and monotonic, then M N lies between R N and L
Question:
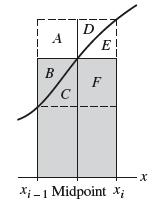
Prove that if ƒ is positive and monotonic, then MN lies between RN and LN and is closer to the actual area under the graph than both RN and LN. In the case that ƒ is increasing, Figure 18 shows that the part of the error in RN due to the ith rectangle is the sum of the areas A + B + D, and for MN it is |B − E|. On the other hand, A ≥ E.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





