Set Im = /2 0 sin m x dx. Use Exercise 69 to prove that Conclude

Set Im = ∫^π/2₀ sin^m x dx. Use Exercise 69 to prove that

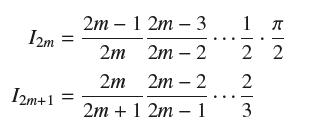
Conclude that

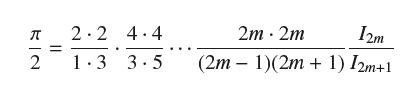
Data From Exercise 69

Let I_m = ∫^π/2₀ sin^m x dx.

(a) Show that I₀ = π/2 and I₁ = 1.
(b) Prove that, for m ≥ 2,

(c) Use (a) and (b) to compute I_m for m = 2, 3, 4, 5.

Transcribed Image Text:

12m 12m+1 = 2m 12m3 2m 2m-2 2m 2m-2 2m + 1 2m 1 N!= KIN 2 2 2|3