Show that for k 1 and x 0, for some polynomial P(x) and some exponent
Question:
Show that for k ≥ 1 and x ≠ 0,
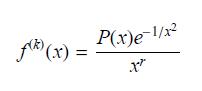
for some polynomial P(x) and some exponent r ≥ 1. Use the result of Exercise 71 to show that ƒ (k)(0) exists and is equal to zero for all k ≥ 1.
Data From Exercise 71
Let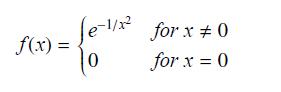
These exercises show that ƒ has an unusual property: All of its derivatives at x = 0 exist and are equal to zero.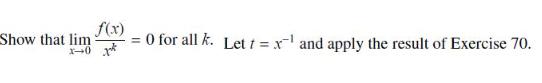
Data From Exercise 70
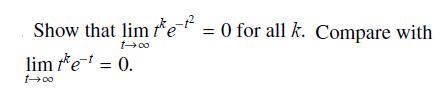
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





