Surfaces of Revolution Let (mathcal{S}) be the surface formed by rotating the region under the (operatorname{graph} z=g(y))
Question:
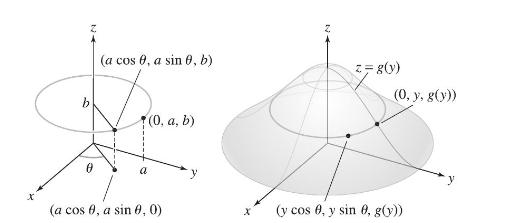
Surfaces of Revolution Let \(\mathcal{S}\) be the surface formed by rotating the region under the \(\operatorname{graph} z=g(y)\) in the \(y z\)-plane for \(c \leq y \leq d\) about the \(z\)-axis, where \(c \geq 0\) (Figure 22).
(a) Show that the circle generated by rotating a point \((0, a, b)\) about the \(z\)-axis is parametrized by
\[
(a \cos \theta, a \sin \theta, b), \quad 0 \leq \theta \leq 2 \pi
\]
(b) Show that \(\mathcal{S}\) is parametrized by
\[
\Phi(y, \theta)=(y \cos \theta, y \sin \theta, g(y))
\]
for \(c \leq y \leq d, 0 \leq \theta \leq 2 \pi\).
(c) Use Eq. (13) to prove the formula
\[
\operatorname{area}(\mathcal{S})=2 \pi \int_{c}^{d} y \sqrt{1+g^{\prime}(y)^{2}} d y
\]
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





