The 1-Dimensional Brouwer Fixed Point Theorem. It indicates that every continuous function mapping the closed interval
Question:
The 1-Dimensional Brouwer Fixed Point Theorem. It indicates that every continuous function ƒ mapping the closed interval [0, 1] to itself must have a fixed point; that is, a point c such that (c) = c.
Show that if ƒ is continuous and 0 ≤ ƒ (x) ≤ 1 for 0 ≤ x ≤ 1, then ƒ(c) = c for some c in [0, 1] (Figure 7).
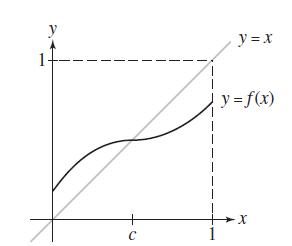
Transcribed Image Text:
1 y с y = x y = f(x) X
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 100% (6 reviews)
If f0 0 the proof is done with c 0 We may assume that f0 0 Let gx fx x g0 f0 0 f0 0 Since f...View the full answer

Answered By

Simon kingori
I am a tier-one market researcher and content developer who has been in this field for the last six years. I’ve run the freelancing gamut; from market research, data mining and SEO/SMM to copywriting, Content Development, you name it, I’ve done it. I’m extremely motivated, organized and disciplined – you have to be to work from home. My experience in Freelancing is invaluable- but what makes me a cut above the rest is my passion to deliver quality results to all my clients- it’s important to note, I've never had a dissatisfied client. Backed by a Masters degree in Computer Science from MOI university, I have the required skill set and burning passion and desire to deliver the best results for my clients. This is the reason why I am a cut above the rest. Having taken a Bsc. in computer science and statistics, I deal with all round fields in the IT category. It is a field i enjoy working in as it is dynamic and new things present themselves every day for research and exploration.
5.00+
1+ Reviews
10+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Mathematics questions
-
The 1-Dimensional Brouwer Fixed Point Theorem. It indicates that every continuous function mapping the closed interval [0, 1] to itself must have a fixed point; that is, a point c such that (c) = c....
-
You have just been engaged as the auditor for Kasempa Company Ltd. During your first audit as the external auditor of the said company, you reviewed the accounting system and procedures operated by...
-
Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...
-
Starting with acetylene as your only source of carbon atoms, identify how you would prepare each member of the following homologous series of aldehydes: a. Ethanal b. Propanal c. Butanal d. Pentanal
-
Disher Cotton Farms is a large cotton producer located near Lubbock, Texas. Each year Disher plants its fields in cotton and then waits until the fall before the cotton is picked and sold. Disher...
-
1. Does Harding have a claim for employment discrimination under ADEA? Why or why not? 2. Would your answer change if Carey was 24, 39, or 45? Explain.
-
Have you intruded into the participants private life?
-
The British government offered physicians incentive pay to offer better customer (patient) service, such as managing appointments better. In particular, physicians can score points by seeing a...
-
Brief Exercise 9-13 (Static) Change in inventory costing methods [LO9-6] In 2021, Hopyard Lumber changed its inventory method from LIFO to FIFO. Inventory at the end of 2020 of $127,000 would have...
-
(a) Assume that g and h are continuous on [a, b]. Use Corollary 2 to show that if g(a) < h(a) and h(b) < g(b), then there exists c [a, b] such that g(c) = h(c). (b) Interpret the result of (a) in...
-
What is the sign of the coefficient multiplying x 7 if is a polynomial of degree 7 such that lim f(x) = o? X-00
-
On June 1, 2013, Hansen Company purchased ten $1,000 Francisco Company bonds at par and classified them as held-to-maturity. In 2014, Francisco experienced financial difficulties and Hansen reduced...
-
The DSV Partnership decided to liquidate as of June 30, 20X5. Its balance sheet as of this date follows: Assets Cash Accounts Receivable (net) Inventories DSV PARTNERSHIP Balance Sheet At June 30,...
-
Below what IQ does .27 of the population fall if the mean is 100 with a standard deviation of 15? (Don't round off IQ score.)
-
1. Can modern day roles be placed in the paradigm of masters, overseers, drivers, and slaves? If so, describe a parallel to these relationships you could interpret through this type of lens. If not,...
-
how could playing in a sandbox help to the development of children? how could a garden help to the development of children? how could playground obstacle courses like a pebble bridge and monkey bars...
-
A store order bottles of shampoo throughout the year. Over time, the store has learned that the annual demand D for shampoo is constant, i.e., there is no variability. Currently, the store decides to...
-
At a total cost of $6,300,000, Veravo Corporation acquired 210,000 shares of Strado Corp. common stock as a long-term investment. Veravo Corporation uses the equity method of accounting for this...
-
Find the center of mass of a thin triangular plate bounded by the y-axis and the lines y = x and y = 2 - x if (x, y) = 6x + 3y + 3.
-
Differentiate the function. (a) f(x) = 240 (b) f(t) = 2 - 2/3t (c) f(x) = x3 - 4x + 6 (d) g(x) = x2 (1 - 2x)
-
Differentiate the function. (a) f(x) = 240 (b) f(t) = 2 - 2/3t (c) f(x) = x3 - 4x + 6 (d) g(x) = x2 (1 - 2x)
-
Differentiate the function. (a) f(x) = 240 (b) f(t) = 2 - 2/3t (c) f(x) = x3 - 4x + 6 (d) g(x) = x2 (1 - 2x)
-
. In explain the problem Distinguish between a meteor, a meteoroid, a meteorite, an asteroid, and a comet
-
Journalize the following adjustments in proper journal entry form please. Account Unadjusted Trial Balance data Income statement data: \begin{tabular}{|lr} \hline Advertising expense & 150,000 \\...
-
Anna is a 20% shareholder in an S corporation. Anna acquired her interest on January 1 of the current year by investing $10,000 for 20% of the corporations stock. In March, the corporation took out a...

Study smarter with the SolutionInn App


