The torque about the origin O due to a force F acting on an object with position vector r is the vector quantity τ = r × F. If several forces Fj act at positions rj, then the net torque (units: N-m or lb-ft) is the sum

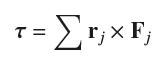
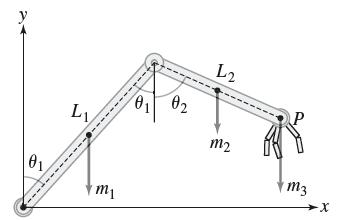
Let τ be the net torque about O acting on the robotic arm of Figure 22, here taking into account the weight of the arms themselves. Assume that the arms have mass m₁ and m₂ (in kilograms) and that a weight of m₃ kg is located at the endpoint P. In calculating the torque, we may assume that the entire mass of each arm segment lies at the midpoint of the arm (its center of mass). Show that the position vectors of the masses m₁, m₂, and m₃ are

= r, ,