Use Exercise 116 to prove the following statements.

(a) G has an inverse with domain R and range {x : x > 0}. Denote the inverse by F.
(b) F(x + y) = F(x)F(y) for all x, y. It suffices to show that G(F(x)F(y)) = G(F(x + y)).
(c) F(r) = Er for all numbers. In particular, F(0) = 1.
(d) F(x) = F(x). Use the formula for the derivative of an inverse function.
This shows that E = e and that F(x) is the function ex as defined in the text.

Data From Exercise 16

Develop an elegant approach to the exponential and logarithm functions. Define a function G for x > 0:

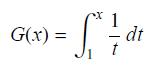
This exercise proceeds as if we didn’t know that G(x) = ln x and shows directly that G has all the basic properties of the logarithm. Prove the following statements.

Transcribed Image Text:

G(x) = S² JI 1 - dt