We investigate how the shape of the limacon curve r = b + cos depends on

We investigate how the shape of the limac¸on curve r = b + cos θ depends on the constant b (see Figure 25).

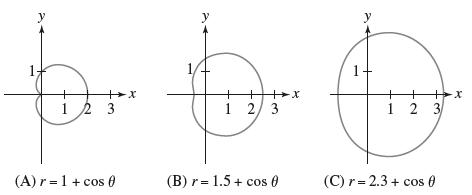
(a) Argue as in Exercise 63 to show that the constants b and −b yield the same curve.
(b) Plot the limac¸on for b = 0, 0.2, 0.5, 0.8, 1 and describe how the curve changes.
(c) Plot the limac¸on for b = 1.2, 1.5, 1.8, 2, 2.4 and describe how the curve changes.
(d) Use Eq. (2) to show that

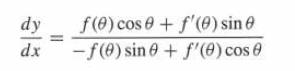
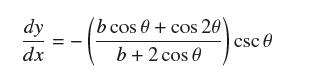
(e) Find the points where the tangent line is vertical. Note that there are three cases: 0 ≤ b 2. Do the plots constructed in (b) and (c) reflect your results?

Transcribed Image Text:

+X 1 2 3 (A) r= 1 + cos 0 + 1 2 3 +X (B) r= 1.5+ cos 0 1 y + 1 2 3 +x (C) r = 2.3 + cos (