Use Green’s Theorem to evaluate the line integral along the given positively oriented curve.

∫_c xe^–2x dx + (x⁴ + 2x²y²) dy, C is the boundary of the region between the circles x² + y² = 1 and x² + y² = 4

Data from Green's Theorem

Let C be a positively oriented, piecewise-smooth, simple closed curve in the plane and let D be the region bounded by C. If P and Q have continuous partial derivatives on an open region that contains D, then

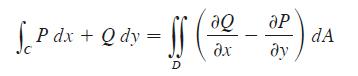
Transcribed Image Text:

If | Pdx + Q dy = D ах ар ду dA