Use Stokes Theorem to evaluate C F dr. In each case C is oriented counterclockwise
Question:
Use Stokes Theorem to evaluate ∫C F · dr. In each case C is oriented counterclockwise as viewed from above.
F(x, y, z) = e–xi + exj + ezk, C is the boundary of the part of the plane 2x + y + 2z = 2 in the first octant
Data from Stokes Theorem
Let S be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve C with positive orientation. Let F be a vector field whose components have continuous partial derivatives on an open region in R3 that contains S. Then
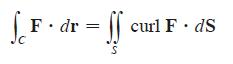
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





