a. The definition of the inverse hyperbolic cosine is y = cosh -1 x x =

Question:

a. The definition of the inverse hyperbolic cosine is y = cosh^-1 x ⇔ x = cosh y, for x ≥ 1, 0 ≤ y < ∞. Use implicit differentiation to show that 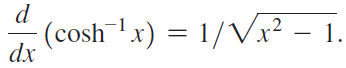:(cosh¯x) = 1/Vx² – 1. dx

b. Differentiate sinh^-1 x = ln (x + √x² + 1) to show that d/dx (sinh^-1 x) = 1/√x² + 1.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Apr 06, 2019 11:56 AM

See More Questions

What is the domain of sech -1 x? How is sech -1 x defined in terms of the inverse hyperbolic cosine?
The inverse hyperbolic sine is defined in several ways; among them are Find the first four terms of the Taylor series for sinh -1 x using these two definitions. dt sinhx = In (x + Vx + 1) V1 + t
State the definition of the hyperbolic cosine and hyperbolic sine functions.
The following information is computed from Fast Food Chains annual report for 2006. 2006 2005 Current assets $ 2,731,020 $ 2,364,916 Property and equipment, net 10,960,286 8,516,833 Intangible...
The Primary Company and the VIE Company had the balance sheet shown in Problem SA2-1 above on the date control was achieved. The Primary Company guaranteed the 5% bond payable issued by the VIE...
Another bank offers 1% increase in interest rate to savings accounts with a balance of more than 10,000.00. Write a future value function Bank1FV(CF, r, n) that reflects this policy. BANK1FV IN...
The Journal of the American Medical Association (Apr. 21, 1993) reported on the results of a National Health Interview Survey designed to determine the prevalence of smoking among U.S. adults. More...
The compensation committee of a large public corporation engages you to help design a tax efficient compensation plan for the current chief executive officer (CEO). In a preliminary interview with...
Adams, Inc. has sales of $100,000 with a contribution margin of $60,000 and net income of $20,000. Baron, Inc. has sales of $110,000 with a contribution margin of $44,000 and net income of $22,000....
On July 1, the ABC Partnership, a calendar-year partnership, distributes to each of its equal partners $10,000 cash and land with a value of $10,000 and a basis of $5,000. A, B and C have outside...
Show that cosh -1 (cosh x) = |x| by using the formula cosh -1 t = ln (t + t 2 - 1) and by considering the cases x 0 and x < 0.
There are several ways to express the indefinite integral of sech x. a. Show that sech x dx = tan -1 (sinh x) + C (Theorem 6.9). Write and then make a change of variables. b. Show that sech x dx =...
Consider two projects, A and B. Project As first cash flow is $7,000 and is received three years from today. Future cash flows for Project A grow by 3 percent in perpetuity. Project Bs first cash...
An epidemiologist plans to conduct a survey to estimate the percentage of women who give birth. How many women must be surveyed in order to be 90% confident that the estimated percentage is in error...
Palmerstown Company established a subsidiary in a foreign country on January 1, Year 1, by investing 8,000,000 pounds when the exchange rate was $1.00/pound. Palmerstown negotiated a bank loan of...
Question 1.Which of the following plans provide the greatest immediate tax benefit for the participating employee? (1) Roth IRA (2) deductible IRA (3) non-deductible IRA (4) 401(k) a. (1) and (3)...
Transcribed image text: 9:13 LTE Done 7 of 7 QUESTION WA AUDION QUESTION 23 = w the tons of a coin comes down heads, you win two dollars. If it comes down tails, you lose fifty cents. How much would...
TRUE or FALSE It is 2016 and the D.C. Circuit has issued its ruling in USTA v. FCC . The D.C. Circuit upheld the 2015 Open Internet Order so the FCC's net neutrality rule stands.True or...
The following data (in millions) are taken from the financial statements of Target Corporation , the owner of Target stores: Year 2 Year 1 Revenue $72,618 $71,279 Operating expenses 67,857 66,320...
A woman at a point A on the shore of a circular lake with radius 2 mi wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible A time. She can walk...
Find an appropriate graphing software viewing window for the given function and use it to display its graph. The window should give a picture of the overall behavior of the function. There is more...
Find an appropriate graphing software viewing window for the given function and use it to display its graph. The window should give a picture of the overall behavior of the function. There is more...
Find the (a) Domain and (b) Range. y = 2e -x - 3
Production numbers for 2 shifts are shown. The shift supervisor of Shift 2 insists to the production manager that her operators are more productive than the ones on Shift 1. Using a confidence level...
In a class, the scores that students got are as shown. What are the 25, 50, 75 and 100th percentiles for the data? 84 84 98 80 89 83 85 56 85 84 84 74 84 81 83 80 45 86 67 79 81 78 76 85 83 77 86 83...
Number of points made by Teams A and B are shown. Which statement is true based on running the F-Test Two-Sample for Variances in the Data Analysis pack in Excel? Use a confidence level of 10% to...

a. The definition of the inverse hyperbolic cosine is y = cosh -1 x x =

Question:

:(cosh¯x) = 1/Vx² – 1. dx

Step by Step Answer:

a Let y coshx Then x co...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions