Question: A well-known method for approximating c for a positive real number c consists of the following recurrence relation (based on Newtons method; see Section 4.8).

A well-known method for approximating √c for a positive real number c consists of the following recurrence relation (based on Newton’s method; see Section 4.8). Let a₀ = c and

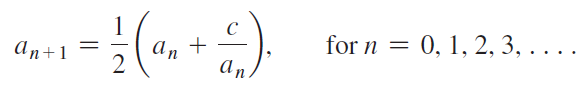
for n = 0, 1, 2, 3, . . . . An An+1

a. Use this recurrence relation to approximate √10. How many terms of the sequence are needed to approximate √10 with an error less than 0.01? How many terms of the sequence are needed to approximate √10 with an error less than 0.0001? To compute the error, assume a calculator gives the exact value.

b. Use this recurrence relation to approximate √c, for c = 2, 3, . . . , 10. Make a table showing the number of terms of the sequence needed to approximate √c with an error less than 0.01.

for n = 0, 1, 2, 3, . . . . An An+1

Step by Step Solution

★★★★★

3.40 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Using the recurrence an1 an n 0 1 2 3 4 5 an 10 55 3659090909 3196005081 3162455622 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

In Section 4.8 we considered Newton's method for approximating a root r of the equation f(x) = 0, and from an initial approximation we obtained successive approximations x2, x3, ...., where Use...

The divide and average? method, an old-time method for approximating the square root of any positive number ? can be formulated as x = x + a/x / 2. (a) Write well-structured pseudosode to implement...

(a) Growth of entire functions. If f(z) is not a constant and is analytic for all (finite) z, and R and M are any positive real numbers (no matter how large), show that there exist values of z for...

1 (Graded). (i) Determine the exact solution to the IVP y' = siWy 11(1) = 2 (ii) Implement the 4stage RungeKutta method given by the Butcher tableau Test it on the IVP from (i J on the interval I [1...

Example 3.36. Consider the IVP (3.88) y' =y y(0) =1 We know that the exact solution is y(x) = e". Let us run Euler's method, say on the interval [0, 1]: (3.89) Un+1 = Un + hF(In, y(x.)) (3.90) Un+1 =...

X 951961..: "Towards a winter tra X + - C ximera.osu.edu/mooculus/higherOrderDerivativesAndGraphs/exercises/exerciseList/higherOrderDerivativesAndGraphs/exercises/higherOrderDerivatives1 H Men Custom...

X Standard form - Ximera X + -> C ximera.osu.edu/mooculus/calculus1TextbookBySection/implicitDifferentiation/implicitDifferentiation/breakGround H Men Custom Suits... BASEXX... O BERHAS 20... b Big...

Applied Mathematics and Computation 95 (1998) 181192 Love dynamics: The case of linear couples Sergio Rinaldi 1 Centro Teoria dei Sistemi, CNR, Politecnico di Milano, Via Ponzio 34/5, 20133 Milan,...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

9/14/10 12:39 PM Page 381 Chapter dug84356_ch06a.qxd 6 Rational Expressions Advanced technical developments have made sports equipment faster, lighter, and more responsive to the human body. Behind...

There are currently 35,000 members covered in a contract with IndyHMO. The pediatric unit where you work is planning a renegotiation effective next January. These negotiations will end up increasing...

A simple well-known game, tic-tac-toe, is played on a three-by-three grid of squares by two players. The players alternate turns. Each player chooses a square and places a mark in a square. (One...

If a comparry had a contribution margin of $ 2 0 0 0 0 0 0 and a contribution margin ratio of 4 0 % , total variable conts must have been $ 3 0 0 0 0 0 0 . $ 1 2 0 0 0 0 0 . $ 5 0 0 0 0 0 0 . $ 6 0 0...

10. Assume that Atlas Sporting Goods, Inc., has $800,000 in assets. If it goes with a low-liquidity plan for the assets, it can earn a return of 15 percent, but with a high-liquidity plan the return...

A force of 200 N will stretch a garage door spring 0.8 m beyond its unstressed length. How far will a 300-N force stretch the spring? How much work does it take to stretch the spring this far from...

How much work has to be performed on a 6.5-oz softball to pitch it 132 ft/sec (90 mph)?

Did you know that if you cut a spherical loaf of bread into slices of equal width, each slice will have the same amount of crust? To see why, suppose the semicircle y = r 2 - x 2 shown here is...

I already understand how to do section a and b, but I do not know how to calculate the Par Yield for section C. Please show your work for this, and thank you for your help. The following table gives...

A stock with a beta of 0.7 is priced at exist118.50 and just paid a dividend of exist2.85. If the risk-free rate is 2% and the market risk premium is 7%, what growth rate does the market expect for...

You are given the following information concerning three portfolios, the market portfolio, and the risk-free asset: Portfolio R p p p X 13.5 % 34 % 1.25 Y 12.5 29 1.10 Z 9.3 19 .70 Market 11.5 24...