Assuming the limit exists, the definition of the derivative If h > 0, then this approximation is

Assuming the limit exists, the definition of the derivative

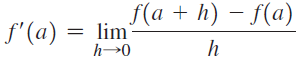
implies that if h is small, then an approximation to f'(a) is given by

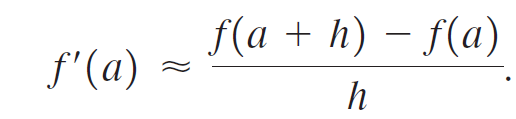
If h > 0, then this approximation is called a forward difference quotient; if h < 0, it is a backward difference quotient. As shown in the following exercises, these formulas are used to approximate f' at a point when f is a complicated function or when f is represented by a set of data points.

Let f(x) = √x.
a. Find the exact value of f'(4).

b. Show that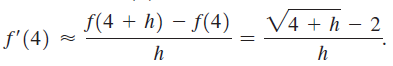 

c. Complete columns 2 and 5 of the following table and describe how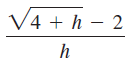behaves as h approaches 0.

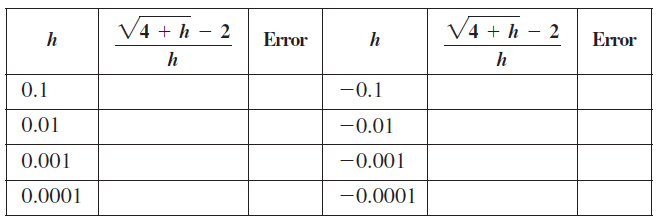
d. The accuracy of an approximation is measured by

error = |exact value - approximate value|

Use the exact value of f'(4) in part (a) to complete columns 3 and 6 in the table. Describe the behavior of the errors as h approaches 0.

Transcribed Image Text:

f(a + h) – f(a) f"(a) lim h. f(a + h) – f(a) f"(a)