Consider series where |r| a. Complete the following table showing the smallest value of n, calling it
Question:
Consider series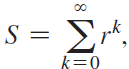 where |r|
where |r|
a. Complete the following table showing the smallest value of n, calling it N(r), such that |S - Sn| -4, for various values of r. For example, with r = 0.5 and S = 2, we find that |S - S13| = 1.2 ? 10-4 and |S - S14| = 6.1 ? 10-5. Therefore, N(0.5) = 14.

b. Make a graph of N(r) for the values of r in part (a).
c. How does the rate of convergence of the geometric series depend on r?
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett
Question Posted:





