Consider the curve r = f() = cos a - 1.5, where a = (1 +

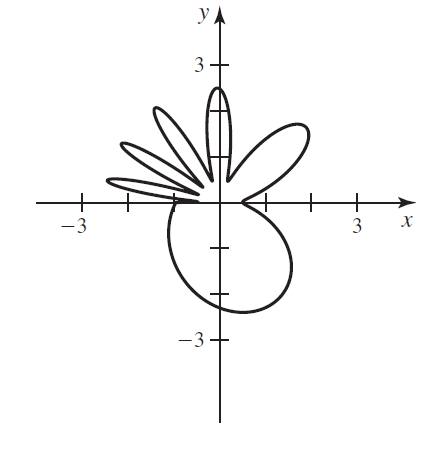
Consider the curve r = f(θ) = cos a^θ - 1.5, where a = (1 + 12π)^1/(2π) ≈ 1.78933 (see figure).

a. Show that f(0) = f(2π) and find the point on the curve that corresponds to θ = 0 and θ = 2π.

b. Is the same curve produced over the intervals [-π, π] and [0, 2π]?

c. Let f(θ) = cos a^θ - b, where a = (1 + 2kπ)1/^(2π), k is an integer, and b is a real number. Show that f(0) = f(2π) and that the curve closes on itself.

d. Plot the curve with various values of k. How many fingers can you produce?

Transcribed Image Text:

Ул 3 -3 3 -3-