Question: Consider the following function and its power series: a. Let S n (x) be the sum of the first n terms of the series. With

Consider the following function and its power series:

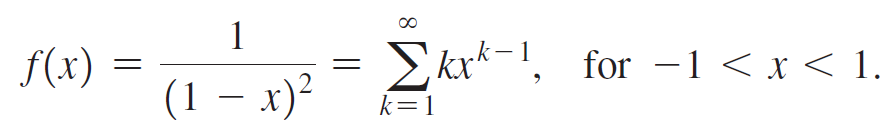
1 Skx*-1, for –1 < x < 1. f(x) (1 – x)² k=1 ||

a. Let S_n(x) be the sum of the first n terms of the series. With n = 5 and n = 10, graph f(x) and S_n(x) at the sample points x = -0.9, -0.8, . . , -0.1, 0, 0.1, . . , 0.8, 0.9 (two graphs). Where is the difference in the graphs the greatest?

b. What value of n is needed to guarantee that |f(x) - S_n(x) |< 0.01 at all of the sample points?

1 Skx*-1, for 1 < x < 1. f(x) (1 x) k=1 ||

Step by Step Solution

★★★★★

3.35 Rating (173 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

For both graphs the difference between the true value and the estimate is greate... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

Consider the following function : (x) = 2x + 3/x Perform 10 iterations of quadratic interpolation to locate the minimum. Comment on the convergence of your results. (x 0 = 0.1, x 1 = 0.5, x 2 = 5)

Consider the following function: f (x) = 48x 60x2 + x3. (a) Use the first and second derivatives to find the local maxima and local minima of f (x). (b) Use the first and second derivatives to show...

Consider the following function: Show that f (x) is convex by expressing it as a sum of functions of one or two variables and then showing (see Appendix 2) that all these functions are convex. fix) =...

Consider the following function. f(x) = In(1 + 4x) Complete the table. f ( n) (0 ) 0 1 4 -8 X 64 X -768 X Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f...

(1 point) For the following function, find the Taylor series centered at c = 2 and then give the first 5 nonzero terms of the Taylor series and the open interval of convergence. f(x) = e37 f(z) = 7 0...

Use the binomial series to expand the following function as a power series. Give the first 3 non-zero terms. 1 h(x) : (4 + x) x2+...

Use the binomial series to expand the following function as a power series. Give the first 3 non-zero terms. 1 h(I) = + I't. . . (4+ 1)7

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Draft a simple contract for a small construction project (remodeling a suite of offices or the interior of a store, for instance) under which a businessperson hires an independent contractor to do...

What is the Internet Crime Computer Center and what does it do?

P5.6 (LO 5) (Purchase Price of a Business) During the past year, Stacy McGill planted a new vineyard on 150 acres of land that she leases for 30,000 a year. She has asked you as her accountant to...

The Politics of Financial Crisis

Find the points on the ellipse x 2 + 2y 2 = 1 where (x, y) = xy has its extreme values.

Find equations for the (a) Tangent plane and (b) Normal line at the point P 0 on the given surface. x 2 + y 2 + z 2 = 3, P 0 (1, 1, 1)

Find the specific function values. (x, y) = sin (xy) a. 2 c. f(1) . 4 b. f (-3.) 12 d. 1. (-)

You own the following portfolio of stocks. What is the portfolio weight of stock C? 64.26 percent 58.02 percent 20.30 percent 35.74 percent 37.72 percent

5. Assume the par value of the bond is $1,000. The Pioneer Petroleum Corporation has a bond outstanding with an $85 annual interest payment, a market price of $800, and a maturity date in five years....

Question 1: Setup [4 marks] Create an active Processing function that draws a spaceship on a dark background. The spaceship is a simple triangle shape that can be turned to point in any direction....