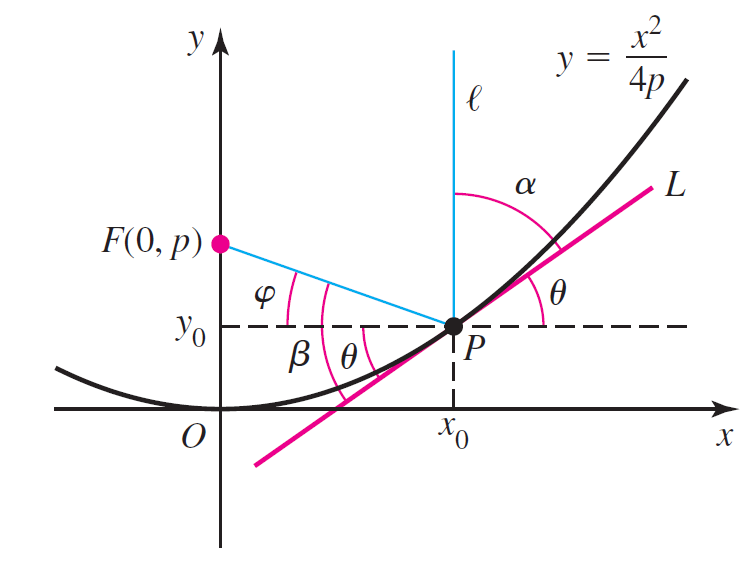
Consider the parabola y = x²/4p with its focus at F(0, p) (see figure). The goal is to show that the angle of incidence between the ray ℓ and the tangent line L (α in the figure) equals the angle of reflection between the line PF and L (β in the figure). If these two angles are equal, then the reflection property is proved because ℓ is reflected through F.

a. Let P(x₀, y₀) be a point on the parabola. Show that the slope of the line tangent to the curve at P is tan θ = x₀/(2p).

b. Show that tan φ = (p - y₀)/x₀.

c. Show that α = π/2 - θ; therefore, tan α = cot θ.

d. Note that β = θ + φ. Use the tangent addition formula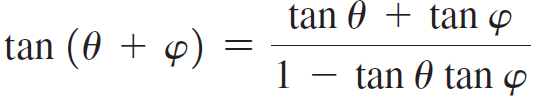to show that tan α = tan β = 2p/x₀.

e. Conclude that because α and β are acute angles, α = β.

Transcribed Image Text:

tan 0 + tan o tan (0 + 4) 1 - tan 0 tan o 4p F(0, p) Ф Уo ПР х