Determine whether the following statements are true and give an explanation or counterexample.

a. The terms of the sequence {a_n} increase in magnitude, so the limit of the sequence does not exist.

b. The terms of the series ∑1/√k approach zero, so the series converges.

c. The terms of the sequence of partial sums of the series ∑a_k approach 5/2 , so the infinite series converges to 5/2.

d. An alternating series that converges absolutely must converge conditionally.

e. The sequenceconverges.

f. The sequenceconverges.

g. The series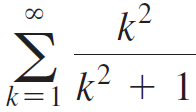converges.

h. The sequence of partial sums associated with the series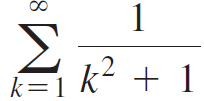converges.

Transcribed Image Text:

п? ап п? + 1 2 (-1)" n² An n² + 1