If the top half of the ellipse x²/a² +y²/b² = 1 is revolved about the x-axis, the result is an ellipsoid whose axis along the x-axis has length 2a, whose axis along the y-axis has length 2b, and whose axis perpendicular to the xy-plane has length 2b. We assume that 0 < b < a (see figure). Use the following steps to find the surface area S of this ellipsoid.

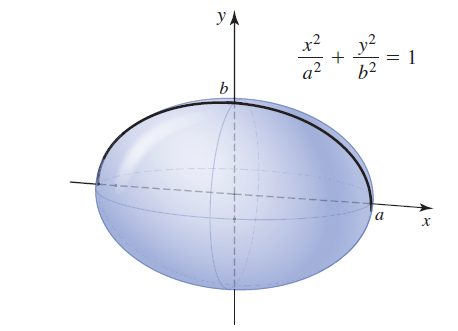
a. Use the surface area formula to show that

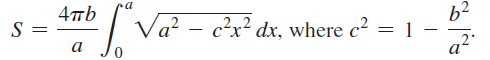
b. Use the change of variables u = cx to show that

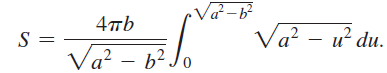
c. A table of integrals shows that

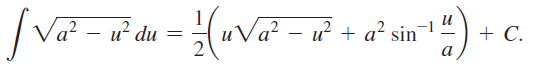
d. If a and b have units of length (say, meters), what are the units of S according to this formula?

e. Use part (a) to show that if a = b, then S = 4πa², which is the surface area of a sphere of radius a.

Transcribed Image Text:

УА q² г9 х 4 тb Va? – c²x² dx, where c² = b2 a2" a