Let f and g be differentiable functions with h(x) f(g(x)) For a given constant a, let u g(a) and v g(x), and define a Show that b For any value of u show that f(v) f(u) (H(v) f '(u))(v u) c Show that d Show that h '(a) f '(g(a))g '(a) f(v) f(u) f'(u) if v u H(v) if v u lim H(v) 0 ...

a b Suppose u v Then clearly both sides of the gi ...

Let f and g be differentiable functions with h(x) = f(g(x)). For a given constant a, let

Question:

Let f and g be differentiable functions with h(x) = f(g(x)). For a given constant a, let u = g(a) and v = g(x), and define

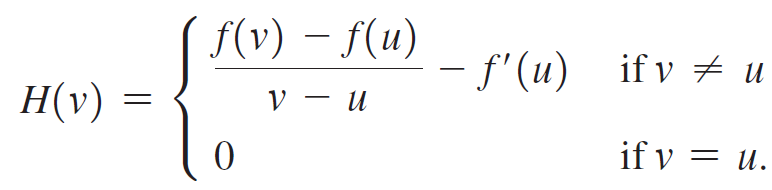
f(v) – f(u) - f'(u) if v # u H(v) if v = u.

a. Show that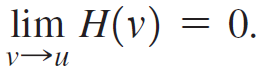 lim H(v) = 0.

b. For any value of u show that

f(v) - f(u) = (H(v) + f'(u))(v - u).

c. Show that

d. Show that h'(a) = f'(g(a))g'(a).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Feb 13, 2019 09:13 AM

Let f: X be differentiable at x and g: Y be differentiable at y. Then their product f g: X Y R is differentiable at (x, y) with derivative Dfg[x, y] = f(x)Dg[y] + g(y) Df[x]
Let f: X be differentiable at x and g: Y be differentiable at y with f(y) 0. Then their quotient f/g: X Ã Y is differentiable at (x, y) with derivative g(y)Df x-f(x)Dg|y] (g(y))? D-x, y)
Let be a continuous real-valued function on the unit circle {x R2 : |x| =1} such that f (0, 1) = g(1, 0) = 0 and g(- x )= - g(x). Define f: R2R by F (x) = {|x| . g (x/|x| x 0, 0 x = 0. (a) If x R2...
Ag Bio Tech (ABT) was organized on January 1, 2013, by four friends. Each organizer invested $10,000 in the company and, in turn, was issued 8,000 shares of common stock. To date, they are the only...
What is the difference between an interim dividend and a final dividend?
What is the quickest way to get help while in Excel?
Explain the accounting entries for the formation of a partnership. LO5
Ronald Naquin, an employee of Air Engineered Systems & Services, Inc., owned one-third of its outstanding shares. After six years, he was fired and an offer was made to buy out his interest in Air...
Bella's Bakery is a privately owned bakery located in Charlottetown, PEI. Bella and her brother, John, opened the bakery in 2018. John was eager to help Bella bring her dream to life after he got his...
Prepare the journal by recording the following transactions 3-Dec Mrs. Veena started business by introducing cash Rs. 5000 and Rs 500000 as transfer from her saving bank account in the business 5-Dec...
Use the definition of the derivative to evaluate the following limits. 5* 25 lim >2 2
Use the definition of the derivative to evaluate the following limits. (3 + h)+h 27 lim
Photovoltaic (PV) cells convert sunlight energy directly into electricity, with no moving parts (recall Fig. 37.21). In a PV cell, photons incident on a semiconductor PN junction promote electrons to...
1. What does the phrase "cost of quality" mean? How might using this statement assist a company in addressing its quality issues? 2. What key distinctions exist between total quality human resource...
Does productivity in terms of output per labor our insure a company will be profitable? Why or why not? What questions should be asked to test whether productivity has increased? How do these answers...
How do the four Ps of marketing (product, price, promotion, place) differ in international markets?
Do you agree with the societal or political forces? Why or why not? Support your assertions with credible sources
How do the global transformational leadership models comprise a work environment that sees the need for change and embraces the new changes?Explain
Research different tools for assessing leadership styles. Summarize at least three tools and the styles they mention. Do you believe that its best for leaders to use different styles in different...
Rewrite Programming Exercise 7.5 using streams. Display the numbers in increasing order. Data from Programming Exercise 7.5 Write a program that reads in 10 numbers and displays the number of...
Assume that all the given functions have continuous second-order partial derivatives. If z = f (x, y), where x = r 2 + s 2 and y = 2rs, find 2z/r s. (Compare with Example 7.)
Assume that all the given functions have continuous second-order partial derivatives. If z = f(x, y), where x = r cos 0 and y = r sin 0, find (a) dz/or, (b) dz/ae, and (c) az/dr d0.
Assume that all the given functions have continuous second-order partial derivatives. Suppose z = f (x, y), where x = g(s, t) and y = h(s, t). (a) Show that (b) Find a similar formula for 2z/s t. ?z ...
Assume that an investment of $100,000 is expected to grow during the next year by 8% with SD 20%, and that the return is normally distributed. Whats the 5% VaR for the investment? A. $24,898 B....
Simpson Ltd is a small IT company, which has 2 million shares outstanding and a share price of $20 per share. The management of Simpson plans to increase debt and suggests it will generate $3 million...
The following are the information of Chun Equipment Company for Year 2 . ( Hint: Some of the items will not appear on either statement, and ending retained earnings must be calculated. ) Salaries...

Let f and g be differentiable functions with h(x) = f(g(x)). For a given constant a, let

Question:

f(v) – f(u) - f'(u) if v # u H(v) if v = u. lim H(v) = 0.

Step by Step Answer:

a b Suppose u v Then clearly both sides of the gi...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions