Question: Let H be the hyperbola x 2 - y 2 = 1 and let S be the 2-by-2 square bisected by the asymptotes of H.

Let H be the hyperbola x² - y² = 1 and let S be the 2-by-2 square bisected by the asymptotes of H. Let R be the anvil-shaped region bounded by the hyperbola and the horizontal lines y = ±p (see figure).

a. For what value of p is the area of R equal to the area of S?

b. For what value of p is the area of R twice the area of S?

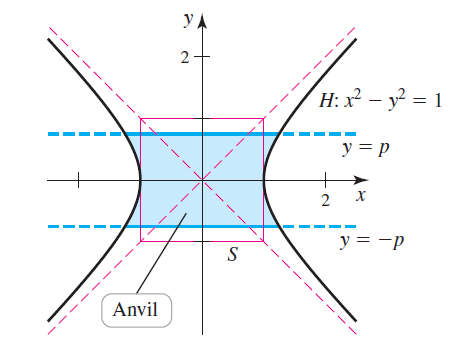
УА Н: 22 — у? %3D 1 y = p х 2 y = -p Anvil -- - --

: 22 ? %3D 1 y = p 2 y = -p Anvil -- - --

Step by Step Solution

★★★★★

3.46 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The area of the anvil is A 4 f 1 y dy 4 ftan p sec t dt 2p1 p 2ln1p p ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus Early Transcendentals Questions!

Let H be the hyperboloid of one sheet, given by x2 + y2 - z2 = 1. a) Use Exercise 11.6.9 to prove that at every point (a, b, c) H, H has a tangent plane whose normal is given by (-a, -b, c). b) Find...

Consider the parametric equations x = a cos t + b sin t, y = c cos t + d sin t, where a, b, c, and d are real numbers. a. Show that (apart from a set of special cases) the equations describe an...

a. Plot the following curves, indicating the positive orientation. b. Eliminate the parameter to obtain an equation in x and y. c. Identify or briefly describe the curve. d. Evaluate dy/dx at the...

HW 111 Hyperbolas A hyperbola is a set of points in a plane the difference of whose distances from two fixed points, called foci, is a constant. * For any point P that is on the hyperbola, d2 - d, is...

Answer all the activities correctly CONTENT DISCUSSIONS Identifying the Conic Section by Inspection The equation of a circle may be written in standard form to megood Ar + Ay' + Ca + Dy 4 E= 0, that...

CONTENT DISCUSSIONS Identifying the Conic Section by Inspection The equation of a circle may be written in standard form to megood Ar + Ay' + Ca + Dy 4 E= 0, that is, the coefficients of a2 and yz...

kndly explain everything I dont understand this lesson and answerr the activity ad also pls explain your answers CONTENT DISCUSSIONS Identifying the Conic Section by Inspection The equation of a...

As a manager of a virtual team, what qualifications and characteristics would you look for in potential team members so that the teams work would be exceptional?

Problem Set: Road Map Problem Br MgBr A B 1)CH;CH2CH Na,Cr207 1) CH3M gBr D E 2) H;O* H,SO4 2) H;0*

How to prepare multiple-period quality trend reports?

=+Do you think these consumers will attend to the Seal in product advertisements?

How do you find the intersection of two lines in space? A line and a plane? Two planes? Give examples.

Let P be a plane in space and let v be a vector. The vector projection of v onto the plane P, proj P v, can be defined informally as follows. Suppose the sun is shining so that its rays are normal to...

Find parametrizations for the line segments joining the points. Draw coordinate axes and sketch each segment, indicating the direction of increasing t for your parametrization. (0, 0, 0), (1, 0, 0)

2 - 7 : ABC Corporation expects to earn $ 2 0 0 , 0 0 0 at the end of the year and projects a growth in earnings of 5 percent per year. If k is 1 0 percent, what is the present value of the earnings...

2) Tri-County Utilities, Inc., supplies natural gas to customers in a three-county area. The company purchases natural gas from two companies: Southern Gas and Northwest Gas. Demand forecasts for the...

Thompson, Ine. In its 2011 income statement, Thompson Inc. reported net income of $1,260 and depreciation expense of $270. On its 2012 income statement, the company reported net income of $2,420 and...