Let The remainder in truncating the power series after n terms is R n (x) f(x) S n (x), which depends on x a Show that R n (x) x n (1 x) b Graph the remainder function on the interval x 1 for n 1, 2, 3 Discuss and interpret the graph Where on the interval is R n (x) largest Smallest c For fixed n, ...

a R fx Snx n This is a geometric series with ratio z Its sum is then R desire ...

Let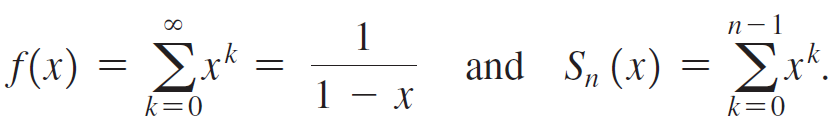 The remainder in truncating the power series after n terms is R n (x) = f(x)

Question:

Let
п— 1 Σr. Σ. and S„ (x) f(x) k=0 k=0

The remainder in truncating the power series after n terms is R_n(x) = f(x) - S_n(x), which depends on x.

a. Show that R_n(x) = xⁿ/(1 - x).

b. Graph the remainder function on the interval |x| < 1 for n = 1, 2, 3. Discuss and interpret the graph. Where on the interval is |R_n(x)| largest? Smallest?

c. For fixed n, minimize |R_n(x)| with respect to x. Does the result agree with the observations in part (b)?

d. Let N(x) be the number of terms required to reduce |R_n(x)| to less than 10^-6. Graph the function N(x) on the interval |x| < 1. Discuss and interpret the graph.

Fantastic news! We've Found the answer you've been seeking!