Recall that the substitution x = a sec implies either x a (in which case 0 < /2 and tan

Recall that the substitution x = a sec θ implies either x ≥ a (in which case 0 ≤ θ < π/2 and tan θ ≥ 0) or x ≤ -a (in which case π/2 < θ ≤ π and tan θ ≤ 0).

Graph the function 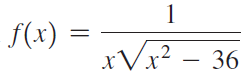on its domain. Then find the area of the region R₁ bounded by the curve and the x-axis on [-12, -12/√3] and the area of the region R₂ bounded by the curve and the x-axis on [12/√3, 12]. Be sure your results are consistent with the graph.

1 f(x) xVx? 36