Scientists often use the logistic growth function to model population growth, where P 0 is the initial
Question:
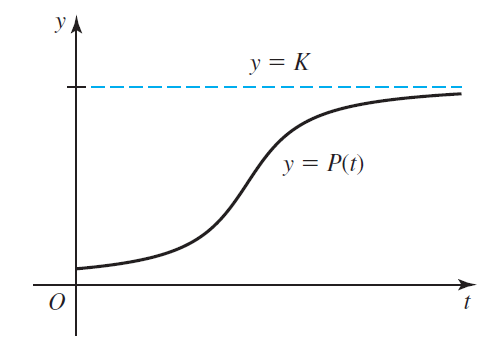
Scientists often use the logistic growth function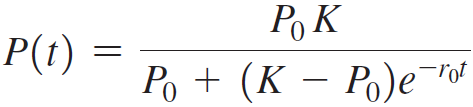 to model population growth, where P0 is the initial population at time t = 0, K is the carrying capacity, and r0 is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model.
to model population growth, where P0 is the initial population at time t = 0, K is the carrying capacity, and r0 is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model.
The population of the world reached 6 billion in 1999 (t = 0). Assume Earth’s carrying capacity is 15 billion and the base growth rate is r0 = 0.025 per year.
a. Write a logistic growth function for the world’s population (in billions) and graph your equation on the interval 0 ≤ t ≤ 200 using a graphing utility.
b. What will the population be in the year 2020? When will it reach 12 billion?
Step by Step Answer:

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett





