Suppose an object of mass m is attached to the end of a spring hanging from the ceiling. The mass is at its equilibrium position y = 0 when the mass hangs at rest. Suppose you push the mass to a position y₀ units above its equilibrium position and release it. As the mass oscillates up and down (neglecting any friction in the system), the position y of the mass after t seconds is

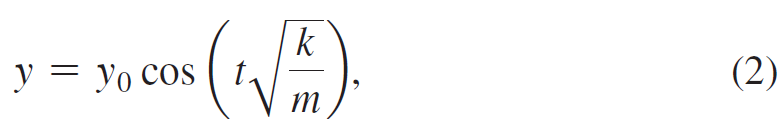
here k > 0 is a constant measuring the stiffness of the spring (the larger the value of k, the stiffer the spring) and y is positive in the upward direction.

Use equation (2) to answer the following questions.

a. The period T is the time required by the mass to complete one oscillation. Show that T = 2π√m/k.

b. Assume k is constant and calculate dT/dm.

c. Give a physical explanation of why dT/dm is positive.

Transcribed Image Text:

у — Уо сOs (2) т