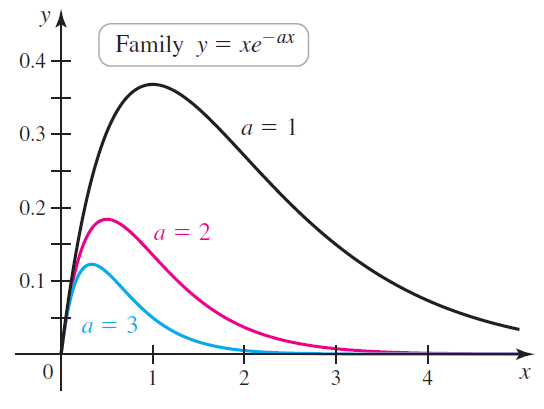
The curves y = xe^-ax are shown in the figure for a = 1, 2, and 3.

a. Find the area of the region bounded by y = xe^-x and the x-axis on the interval [0, 4].

b. Find the area of the region bounded by y = xe^-ax and the x-axis on the interval [0, 4], where a > 0.

c. Find the area of the region bounded by y = xe^-ax and the x-axis on the interval [0, b]. Because this area depends on a and b, we call it A(a, b), where a > 0 and b > 0.

d. Use part (c) to show that A(1, ln b) = 4A(2, (ln b)/2).

e. Does this pattern continue? Is it true that A(1, ln b) = a²A(a, (ln b)/a)?

Transcribed Image Text:

У, Family y = xe ax 0.4 a = 1 0.3 0.2 a = 2 0.1 ↑ a = 3 4 3.