The right-sided and left-sided derivatives of a function at a point a are given by respectively, provided

Question:

The right-sided and left-sided derivatives of a function at a point a are given by

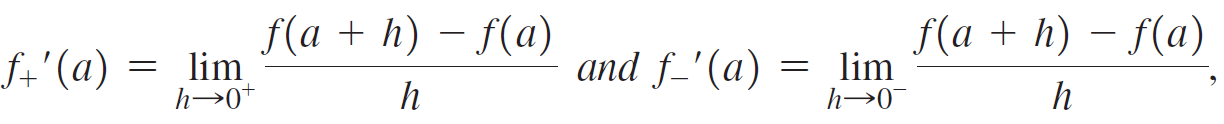
f(a + h) – f(a) lim f(a + h) – f(a) lim f+'(a) and f-'(a) h→0+

respectively, provided these limits exist. The derivative f'(a) exists if and only if f₊'(a) = f_-'(a).

a. Sketch the following functions.

b. Compute f₊'(a) and f_-'(a) at the given point a.

c. Is f continuous at a? Is f differentiable at a?

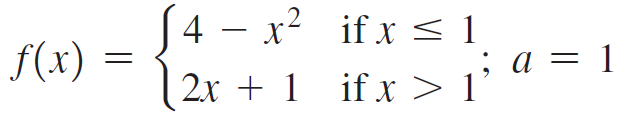
f(x) [ 4 – x² if x < 1 2x + 1 ifx > l’

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Feb 08, 2019 11:48 AM

See More Questions

A vertical line intersects the graph of a function at most once.
What are the second and third derivatives of a function f? If f is the position function of an object, how can you interpret and f?
If f is continuous on [a, b] and there exist numbers a such that holds for all c (a, b), prove that f(x) = 0 for all x [a, b]. .b f(x) dx + | f (x) dx = 0
4. Finally, briefly discuss how you could use an empirical econometric model to assess the health and economic growth consequences of a 'fat tax'.
Family Appliance Mart Ltd. began operations on May 1 and uses a perpetual inventory system. During May, the company had the following purchases and sales for one of its products: Instructions (a)...
The late Nobel Laureate James Buchanan, who was one of the key figures in developing the public choice model, wrote, "The relevant difference between markets and politics does not lie in the kinds of...
Sketch the sampling distribution of (j3, - i3,) based on independent random samples of n, = 100 and n, = 200 observations from two binomial populations with successprobabilities j3, = .1 and j3, =...
Why are accountants so concerned about their organization having an efficient and effective internal control system?
Huron Company produces a commercial cleaning compound known as Zoom. The direct materials and direct labor standards for one unit of Zoom are given below. Standard Quantity or Hours 7.40 pounds 0.45...
26. A point object of mass m is connected to a cylinder of radius R via a massless rope. At time t = 0, the object is moving with an initial velocity vo perpendicular to the rope, the rope has a...
The right-sided and left-sided derivatives of a function at a point a are given by respectively, provided these limits exist. The derivative f'(a) exists if and only if f + '(a) = f - '(a). a. Sketch...
If a function f is continuous at a and then the curve y = f(x) has a vertical tangent line at a and the equation of the tangent line is x = a. If a is an endpoint of a domain, then the appropriate...
Which of the following is true? (a) The Internet is faster than most local area networks. (b) Most metropolitan networks are faster than the Internet. (c) The speed of the Internet is usually...
1) Factor the following Expressions (Write your factors only, don't show your work) a) 2x - 32 = c) 3x-2x-8= b) 2x-6x-8=
Bloomfield Inc. manufactures widgets. A major piece of equipment used to make the widget is nearing the end of its useful life. The company is trying to decide whether they should lease new equipment...
1. a. What is network management? Illustrate network management functional flowchart. [2.5] b. What encoding and decoding mechanisms are used in fast Ethernet and gigabit Ethernet? What is meant by...
Project Data: Sam Parker owns and operates a consulting firm called Business Solutions. The business began operating in October 202X. Transactions for October and November 202X have been recorded and...
3. Use Hooke's law to predict which one out of each pair vibrates at a higher wavenumber. Explain your answer. (7 points) a) C-H and C-D* b) C-C and C=C where: 1 k v = 2, v=wavenumber c = velocity of...
Calculate the flux of energy arising from a temperature gradient of 10.5Km 1 in a sample of argon in which the mean temperature is 280K.
What is the back work ratio? What are typical back work ratio values for gas-turbine engines?
Evaluate the integral. t sin?t dt
Evaluate the integral. x sin'x dx
Evaluate the integral. tan x sec' x dx
Discuss why it is important for company managers to understand and use social capital knowledge to help build social ties among their skilled knowledge workers so they can build employee loyalty...
Kate lives in a house close to a local university, and she traditionally has rented a garage apartment in the back of her property to students for $750 per month. Kate wants to transfer the title to...
Pottery Ranch Inc. has been manufacturing its own finials for its curtain rods. The company is currently operating at 100% of capacity, and variable manufacturing overhead is charged to production at...

The right-sided and left-sided derivatives of a function at a point a are given by respectively, provided

Question:

f(a + h) – f(a) lim f(a + h) – f(a) lim f+'(a) and f-'(a) h→0+ f(x) [ 4 – x² if x < 1 2x + 1 ifx > l’ " ; a = 1

Step by Step Answer:

a b Assuming the point a 1 we get because for h 0 we have 1 h ...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions