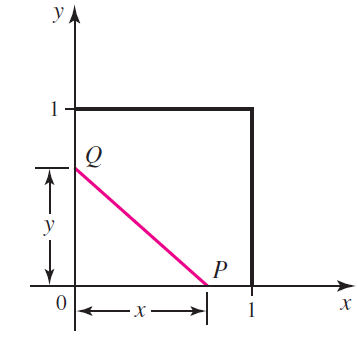
Two points P and Q are chosen randomly, one on each of two adjacent sides of a unit square (see figure). What is the probability that the area of the triangle formed by the sides of the square and the line segment PQ is less than one-fourth the area of the square? Begin by showing that x and y must satisfy xy < 1/2 in order for the area condition to be met. Then argue that the required probability is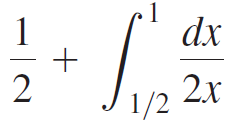and evaluate
the integral.

dx 2x 1/2 1 P -