A mathematician exploring the relationship between ratings of movies, their year of release, and their length discovered a paradox. Rather than list the data set of 100 movies in the original research, we have created a sample of size 10 that captures the properties of the original dataset. In the table below, the rating is a score from 1 to 10, and the length is in minutes.

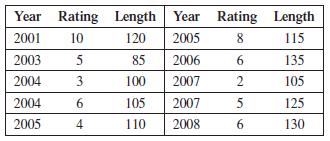
(a) Find the correlation coefficient between the years since 2000 and the length.

(b) Find the correlation coefficient between the length and the rating.
(c) Given that you found a positive correlation between the and the length in part (a), and a positive correlation between the length and the rating in part (b), what would you expect about the correlation between the year and the rating? Calculate this correlation. Are you surprised?

(d) Discuss the paradoxical result in part (c). Write what each correlation tells you. Try to explain what is happening. You may want to look at a scatterplot between the year and the rating, and consider which points on the scatterplot represent movies of length no more than 110 minutes, and which represent movies of length 115 minutes or more.

Transcribed Image Text:

Year Rating Length 2001 10 120 85 100 105 110 2003 2004 2004 2005 5 3 6 4 Year Year 2005 2006 2007 2007 2008 Rating Rating Length 8 115 6 2 5 6 135 105 125 130