A study defined administrative intensity as the number of administrative personnel A per production personnel X, or I = A/X. To seek the optimum administrative intensity for an industry, the following production function was defined: Q = CS^σ A^αK^βX^γ, where S is the number of distinct occupational specialties represented in the labor force, s is the marginal relative productivity of specialization, K is the total productive capital, and C is a constant of proportionality.

(a) Unlike the production functions described in this chapter, for which α + β + γ = 1, the study assumed that increasing cumulative control losses result in decreasing returns to scale, so that α + β + γ = 1 - λ, where λ is the control loss parameter. The study also defined k = K/X as the capital intensity per worker. Show that the production function can then be rewritten as Q = CS^σI^αk^βX^1-λ.

(b) The study showed that the profit P can be written as P = (p - r)Q - W₀S - W₁A - F, where p is the market price per unit, r is the production cost per unit, W₀ is the average wage per production worker, W₁ is the average salary per administrative worker, and F is the fixed costs. Letting A = XI in the equation for P, show that ∂P/∂I = 0 (which leads to the maximum profit) when the administrative intensity is given by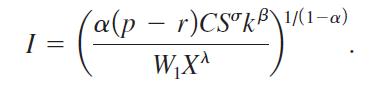

(c) Marginal productivity of administration is given by ∂Q/∂A. Show that this can be written as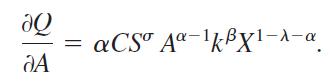

(d) If x and y are functions of z, and ƒ is a function of x, y, and z, the total differential for three variables (to be discussed later in this chapter) can be converted to the chain rule for three variables: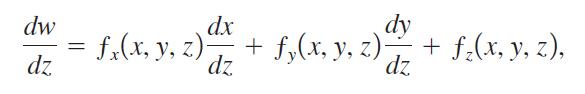

which gives the total rate of change of w with respect to z. Use this result plus the result from part (c) to show that the total rate of change of the marginal productivity of administration with respect to the number of workers can be given as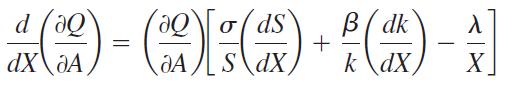

when S and k are both functions of X.

Transcribed Image Text:

W₁X^ 1 (F485 (0-1)/(¹ d)x, = (alp = I