As we saw in Chapter 3, a group of MIT professors created a function for transforming student test scores of 0 to 100 into scores from 0 to 5, with transformed scores concentrated around 3, 4, and 5. Transformed scores from 4.5 to 5 became grades of A, 3.5 to 4.5 became B, and 2.5 to 3.5 became C. They used the following function: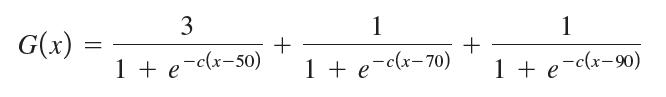

using the value c = 0.7.

(a) Show that G′(x) is always positive, thus verifying that the function is increasing. Explain how you could have drawn this conclusion without any calculus by studying the original function.
(b) From a graphing calculator graph of the function on the interval 0 ≤ x ≤ 100, estimate intervals where the derivative is close to 0.
(c) From the graphing calculator graph used in part (b), estimate all inflection points.
(d) To understand why the function is so flat when x is not close to 50, 70, or 90, show that the derivative can be rewritten as

If x is much bigger or smaller than 50, what can you say about the first term? Make similar observations about the second and third terms.

Transcribed Image Text:

G(x) = 3 1 + e-c(x-50) + 1 1 + e-c(x-70) + 1 1 + e-c(x-90)