In Exercises 40 through 49, assume that the required extreme value is a relative extremum.

The beautiful patterns on the wings of butterflies have long been a subject of curiosity and scientific study. Mathematical models used to study these patterns often focus on determining the level of morphogen (a chemical that effects change). In a model dealing with eyespot patterns,* a quantity of morphogen is released from an eyespot and the morphogen concentration t days later is given by

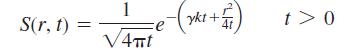
where r measures the radius of the region on the wing affected by the morphogen, and k and γ are positive constants.

a. Find t_m so that ∂S/∂t = 0. Show that the function Sm(t) formed from S(r, t) by fixing r has a relative maximum at t_m. Is this the same as saying that the function of two variables S(r, t) has a relative maximum?

b. Let M(r) denote the maximum found in part (a); that is, M(r) = S(r, t_m). Find an expression for M in terms of z = (1 + 4γkr²)^1/2.

Transcribed Image Text:

S(r, t) 1 :e √4nt e - (y^² + 471) t> 0