In physics, a major area of study is electricity, including such concepts as electric charge, electric force, and electric current. Two ideas that physicists use a great deal are electric potential and electric field. Electric potential is the same as voltage, such as for a battery. Electric field can be thought of in terms of a force field, which is often referred to in space movies as a deflector shield around a spaceship. An electric field causes an electric force to act on charged objects when they are in the electric field. Both electric potential and electric field are produced by electric charges. It is important to physicists and electrical engineers to know what the electric field and the electric potential are near a charged object. Usually the problem involves finding the electric potential and taking the (negative) derivative of the electric potential to determine the electric field. More explicitly,

where V is the electric potential (voltage) near the charged object, z is the distance from the object, and E is the electric field. Let’s look at an example. Suppose we have a charged disk of radius R and we want to determine the electric potential and electric field at a distance z along the axis of the disk (Figure 1).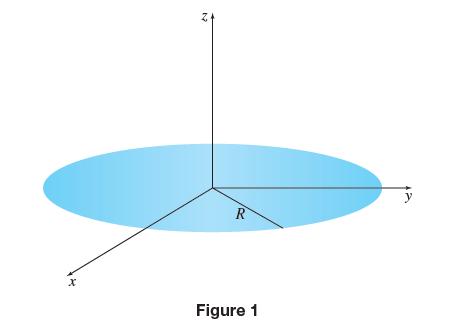

Using some basic definitions and integral calculus (that you will learn about later in your calculus book), it can be shown that the electric potential on the axis is

where k₁ is a constant.* To determine the electric field, we apply Equation (1) and find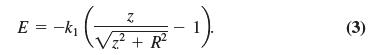

You will provide the details for this example by working through Exercise 1 at the end of this section. Physicists often like to see if complicated expressions such as these can be simplified when certain conditions apply. An example would be to imagine that the location z is very far away from the disk. In that case, the disk doesn’t look much like a disk anymore, but more like a point. In Equations (2) and (3), we see that z will be much larger than R. If you reach the topic of Taylor series in calculus, you will learn how these series can be used to approximate square roots, so that for large values of z the voltage is inversely proportional to z and looks like this:

where k₂ is a constant. To determine the electric field, we apply Equation (1) again to find

You will be asked to prove this result in Exercise 2. Thus we see that the exact functions for V and E of the disk become much simpler at locations far away from the disk. The voltage is a reciprocal function and the electric field is called an inverse-square law. By the way, these functions are the same ones that would be used for a point charge, which is a charge that takes up very little space. Now let’s look at what happens when we are very close to the surface of the disk. You could imagine that an observer very close to the surface would see the disk as a large flat plane. If we apply the Taylor series once more to the exact function for the potential (Equation (2)), but this time with z much smaller than R, we find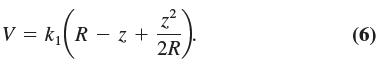

* For those interested in the constants k₁ and k₂: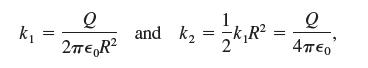

where Q is the charge, ϵ₀ is called the electric permittivity, and R is the radius of the disk.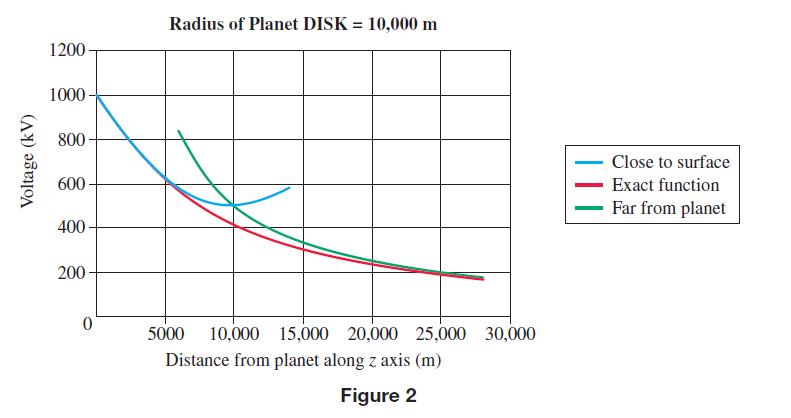

Notice that this is a quadratic function, or a parabola. Applying Equation (1) again, we see that the electric field is

This is just a linear function that increases as we approach the surface (which would be z = 0) and decreases the farther away from the surface we move. Again, the details of this calculation are left for you to do in Exercise 3. Here is a fun way of making sense of the equations listed above. Suppose you are in a spaceship approaching the planet DISK on a very important mission. Planet DISK is noted for the fact that there is always a sizeable amount of charge on it. You are approaching the planet from very far away along its axis. In Figure 2 the three voltage functions (Equations (2), (4), and (6)) are plotted, and in Figure 3 the three electric field functions (Equations (3), (5), and (7)) are plotted. The graphs were generated using R = 10,000, k₁ = 100, and k₂ = 5 * 109.

Notice that it looks as though you can use the reciprocal function for the voltage (Equation (4)) and the inverse-square law function for the electric field (Equation (5)) when you are farther away than about 20,000 m because the exact functions and the approximate functions are almost exactly the same. Also, when you get close to the planet, say less than about 4000 m, you can use the quadratic function for the voltage (Equation (6)) and the linear function for the electric field (Equation (7)) because the exact functions and the approximate functions are nearly the same. This means that you should use the exact functions (Equations (2) and (3)) between about 20,000 m and about 4000 m because the other functions deviate substantially in that region.
There are many other examples that could be studied, but they involve other functions that you haven’t covered yet, especially trigonometric functions. But the process is still the same: If you can determine the electric potential in the region around a charged object, then the electric field is found by taking the negative derivative of the electric potential.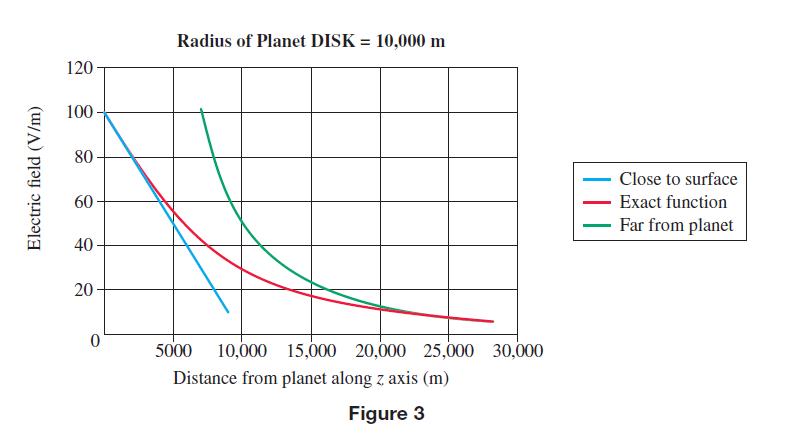

1. Use Equation (1) to prove that the electric field of the disk (Equation (3)) is obtained from the voltage of the disk (Equation (2)).
2. Apply Equation (1) to the voltage of a point charge (Equation (4)) to obtain the electric field of a point charge (Equation (5)).
3. Show that the electric field in Equation (7) results from the electric potential in Equation (6).
4. Sometimes for z very, very close to the disk, the third term in Equation (6) is so small that it can be dismissed. Show that the electric field is constant for this case

Transcribed Image Text:

E = AP dz.' (1)