Suppose that 0 < N < y 0 . Let b = (y 0 - N)/y 0
Question:
Suppose that 0 < N < y0 . Let b = (y0 - N)/y0 and let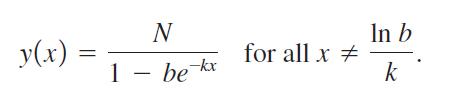
See the figure. Show the following.
(a) 0 < b < 1
(b) The lines y = 0 and y = N are horizontal asymptotes of the graph.
(c) The line x = (ln b)/k is a vertical asymptote of the graph.
(d) y(x) is decreasing on ((ln b)/k, ∞) and on (-∞, (ln b)/k).
(e) y(x) is concave upward on ((ln b)/k, ∞) and concave downward on (-∞, (ln b)/k).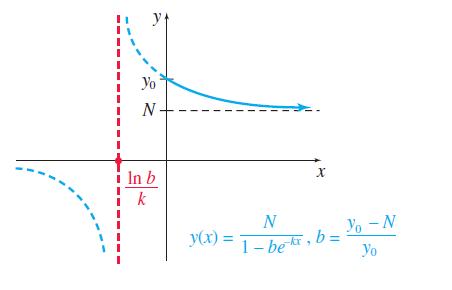
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





