The body’s system of blood vessels is made up of arteries, arterioles, capillaries, and veins. The transport of blood from the heart through all organs of the body and back to the heart should be as efficient as possible. One way this can be done is by having large enough blood vessels to avoid turbulence, with blood cells small enough to minimize viscosity.

We will find the value of angle 0 (see the figure) such that total resistance to the flow of blood is minimized. Assume that a main vessel of radius r₁ runs along the horizontal line from A to B. A side artery, of radius r₂, heads for a point C. Choose point B so that CB is perpendicular to AB. Let CB = s and let D be the point where the axis of the branching vessel cuts the axis of the main vessel.

According to Poiseuille’s law, the resistance R in the system is proportional to the length L of the vessel and inversely proportional to the fourth power of the radius r. That is,

where k is a constant determined by the viscosity of the blood. Let AB = L₀ , AD = L₁ , and DC = L₂.

(a) Use right triangle BDC to find sin θ.
(b) Solve the result of part (a) for L₂.
(c) Find cot u in terms of s and L₀ - L₁.
(d) Solve the result of part (c) for L₁.
(e) Write an expression similar to Equation (1) for the resistance R₁ along AD.
(f) Write a formula for the resistance along DC.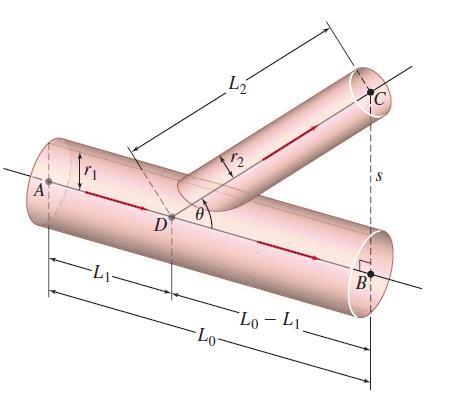

(g) The total resistance R is given by the sum of the resistances along AD and DC. Use your answers to parts (e) and (f) to write an expression for R.

(h) In your formula for R, replace L₁ with the result of part (d) and L₂ with the result of part (b). Simplify your answer.

(i) Find dR/du. Simplify your answer. 

(j) Set dR/dθ equal to 0.

(k) Multiply through by (sin² θ)/s.

(l) Solve for cos θ.

(m) Suppose r₁ = 1 cm and r₂ = 1/4 cm. Find cos θ and then find θ.

(n) Find 0 if r₁ = 1.4 cm and r₂ = 0.8 cm.

Transcribed Image Text:

R = k.. (1)