The figure shows the blood flow in a small artery of the body. The flow of blood is laminar (in layers), with the velocity very low near the artery walls and highest in the center of the artery. In this model of blood flow, we calculate the total flow in the artery by thinking of the flow as being made up of many layers of concentric tubes sliding one on the other.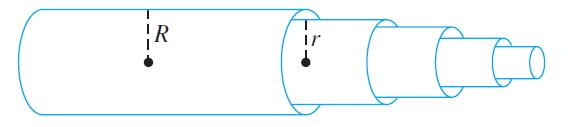

Suppose R is the radius of an artery and r is the distance from a given layer to the center. Then according to Poiseuille’s Law, the velocity of blood in the layer is given by v(r) = k(R² - r²), where k is a numerical constant.

Since the area of a circle is A = πr², the change in the area of the cross section of one of the layers, corresponding to a small change in the radius, Δr, can be approximated by differentials. For dr = Δr, the differential of the area A is dA = 2πr dr = 2πr Δr, where Δr is the thickness of the layer. The total flow in the layer is defined to be the product of velocity and cross-section area, or F(r) = 2πrk(R² - r²)Δr. 

(a) Set up a definite integral to find the total flow in the artery.
(b) Evaluate this definite integral.

Transcribed Image Text:

ㄸ 600