The stage of a new local theater has a rectangular opening, which is 20 m wide and 10 m high. A curtain is to be draped into triangles on the sides, extending from the top to the floor, with a semicircle in the center, as shown in the figure.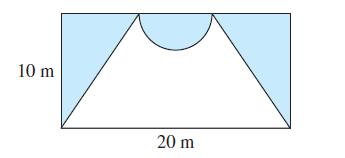

(a) If the radius of the semicircle is r, show that the area of the curtain is

(b) What radius will minimize the area covered by the curtain (and thereby maximize the viewing area)?

(c) Calculate the arc length of the boundary of the semicircular curtain, and compare the length with the height of the stage.

(d) Suppose that the curtain is to contain two semicircles of equal radius in the center, as shown in the figure below. Verify that, if the radius of each semicircle is r, the area of the curtain is A(r) = πr² + 10(10 - 2r), for 0 ≤ r ≤ 5. What radius will minimize the area covered by the curtain? What is the arc length of the boundary of each semicircular curtain?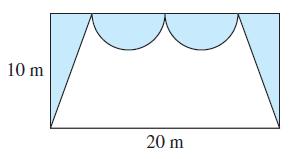

(e) The authors of the paper in The College Mathematics Journal prove that when the curtains of a rectangular stage opening are draped so that triangles form on the left and right sides and semicircles form in the remaining gap across the top, to maximize the viewing area, the arc length of each semicircle should equal the stage height, regardless of the number of semicircles or the stage width (unless it is too small to accommodate the desired number of semicircles). Verify this is true for a curtain draped with three semicircles.

Transcribed Image Text:

10 m 20 m