7.25 Generalizations of the linear-by-linear model (7.11) analyze association between ordinal variables X and Y while controlling
Question:
7.25 Generalizations of the linear-by-linear model (7.11) analyze association between ordinal variables X and Y while controlling for a categorical variable that may be nominal or ordinal. The model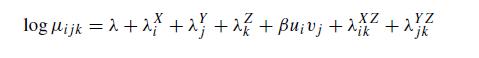
with ordered scores {ui } and {vj } is a special case of model (XY, XZ, YZ) that replaces λXY ij by a linear-by-linear term.
a. Show that the XY conditional independence model (XZ, YZ) is a special case of this model.
b. Assuming the ordinal model, explain how one could construct a test with df = 1 for testing XY conditional independence.
c. For this model, equation (7.12) applies for the cells at each fixed level of Z.
With unit-spaced scores, explain why the model implies that every local odds ratio in each partial table equals exp(β).
d. If we replace β in this model by βk, is there homogeneous association?
Why or why not? (The fit of this model is equivalent to fitting the L × L association model separately for each partial table.)
Step by Step Answer:







