For ordinal square I × I tables of counts {n_ab}, model (12.3) for binary matched-pairs responses (Y_i1, Y_i2) for subject i extends to

logit[P(Y_it ‰¤ j|u_i)] = α_j + βx_t + u_i

with {u_i} independent N(0, σ²) variates and x₁ = 0 and x₂ = 1.

a. Explain how to interpret β, and compare to the interpretation of β in the corresponding marginal model (10.14).

b. This model implies model (12.3) for each 2 × 2 collapsing that combines categories 1 through j for one outcome and categories j + 1 through I for the other. Use the form of the conditional ML (or random effects ML) estimator for binary matched pairs to explain why

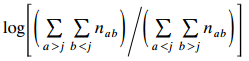j log Σ a>j b

is a consistent estimator of β.

c. Treat these (I €“ 1) collapsed 2 × 2 tables naively as if they are independent samples. Show that adding the numerators and adding the denominators of the separate estimates of e^β motivates the summary estimator of β,

Explain why β̃ is consistent for β even recognizing the actual dependence.

" . nb a j log a>j b b b>a