Let y_it = 1 or 0 for observation t on subject i, i = 1,..., n, t = 1, ..., T. Let y_.t = ?_i y_it/n, y_i. = ?_t y_it/T, and y_.. = ?_i ?_t y_it/nT.

a. Regard {y_i+} as fixed. Suppose that each way to allocate the y_i+ ?successes? to y_i+ of the observations is equally likely. Show that E(Y_it) = y_i, var(Y_it) = y_i.(1 ? y_i), and cov(Y_it, Y_ik) = ? y_i.(1 ? y_i.)/(T ? 1) for t ? k. [The covariance is the same for any pair of cells in the same row, and var(?_t Y_it) = 0 since y_i+ is fixed.]

b. Refer to part (a). For large n with independent subjects, explain why (Y_.1,..., Y_.T) is approximately multivariate normal with pairwise correlation ? = ?1/(T ? 1). Conclude that Cochran?s Q statistic (Cochran 1950)

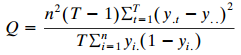
is approximately chi-squared with df = (T ? 1). [One way notes that if (X₁,..., X_T) is multivariate normal with common mean and common variance ?² and common correlation ? for pairs (X_t, X_k), then ?(X_t ? X?)²/?²(1 ? ?) is chi-squared with df = (T ? 1). See Bhapkar and Somes (1977) for slightly weaker conditions for a chi-squared limiting distribution for Q than those in part (a).]

c. Show that Q is unaffected by deleting cases in which y_i1 = ... = y_iT.

n? (T - 1) (y - y.)' .(1- y )