One question in the 1990 General Social Survey asked subjects how many times they had sexual intercourse in the preceding month. Table 13.9 shows responses, classified by gender.

a. The sample means were 5.9 for males and 4.3 for females; the sample variances were 54.8 and 34.4. The mode for each gender was 0. Does an ordinary Poisson GLM seem appropriate? Explain.

b. The Poisson GLM with log link and a dummy variable for gender (1 = males, 0 = females) has gender estimate 0.308 (SE = 0.038). Explain why this implies a ratio of 1.36 for the fitted means. (This is also the ratio of sample means, since this model has fitted means equal to sample means.) Show that the WaId 95% confidence interval for the ratio of means for males and females is (1.26, 1.47).

c. For the negative binomial model, the log likelihood increases by 248.7 (deviance decreases by 497.3). The estimated difference between the log means is also 0.308, but now SE = 0.127. Show that the 95% confidence interval for the ratio of means is (1.06, 1.75). Compare to the Poisson GLM, and interpret.

Table 13.9:

Transcribed Image Text:

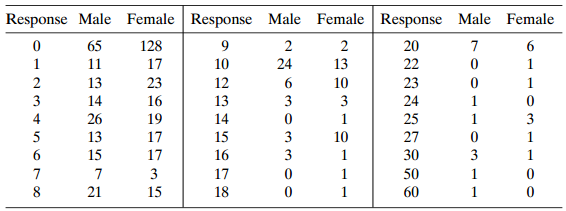
Response Male Female Response Male Female Response Male Female 128 17 23 16 19 2 24 2 13 10 3 20 22 23 24 25 27 30 65 11 13 14 26 13 15 10 12 13 14 15 16 3 3 4 3 3 3 17 17 3 15 10 3 1 1. 17 18 50 60 21