Table 5.17 shows estimated effects for a logistic regression model with squamous cell esophageal cancer (Y = 1, yes; Y = 0, no) as the response. Smoking status (S) equals 1 for at least one pack per day and 0 otherwise, alcohol consumption (A) equals the average number of alcoholic drinks consumed per day, and race (R) equals 1 for blacks and 0 for whites. To describe the race × smoking interaction, construct the prediction equation when R = 1 and again when R = 0. Find the fitted YS conditional odds ratio for each case. Similarly, construct the prediction equation when S = 1 and again when S = 0. Find the fitted YR conditional odds ratios. Note that for each association, the coefficient of the cross-product term is the difference between the log odds ratios at the two fixed levels for the other variable. Explain why the coefficient of S represents the log odds ratio between Y and S for whites. To what hypotheses do the P-values for R and S refer?

Table 5.17:

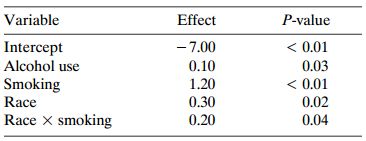
Variable Effect P-value < 0.01 0.03 < 0.01 Intercept Alcohol use Smoking Race Race X smoking - 7.00 0.10 1.20 0.30 0.02 0.20 0.04