A \(25.0 \mathrm{~cm}\) long column packed with silica gel is in equilibrium with a liquid that is 0.0008 wt. frac. toluene and \(0.9992 \mathrm{wt}\). frac \(\mathrm{n}\)-heptane at \(0^{\circ} \mathrm{C}\). Heptane does not adsorb. Toluene equilibrium is \(\mathrm{q}=\mathrm{Kx}\) ( \(\mathrm{q}=\mathrm{g}\) toluene \(/ \mathrm{g}\) adsorbent, \(\mathrm{x}=\mathrm{wt}\) frac toluene in liquid), where \(\mathrm{K}=\) 17.46 at \(0^{\circ} \mathrm{C}\) and \(\mathrm{K}=5.16\) at \(35^{\circ} \mathrm{C}\). Starting at \(8: 00\) a.m., the column is eluted with pure nheptane at \(35^{\circ} \mathrm{C}\) and a superficial velocity of \(10.0 \mathrm{~cm} / \mathrm{min}\). Data are in Problem 20.D4.

Problem 20.D4

A thermal swing adsorption process is removing traces of toluene from n-heptane using silica gel adsorbent. Operation is at \(1.0 \mathrm{~atm}\). Feed is \(0.11 \mathrm{wt} \%\) toluene and \(99.89 \mathrm{wt} \% \mathrm{n}-\) heptane at \(0^{\circ} \mathrm{C}\). Feed step is continued until breakthrough occurs. Adsorber is 2.0 meters long and during feed step is at \(0^{\circ} \mathrm{C}\). Purge is counterflow with pure \(\mathrm{n}\)-heptane at \(80^{\circ} \mathrm{C}\). Column is cooled to \(0^{\circ} \mathrm{C}\) before next feed step. Superficial velocity is \(10.0 \mathrm{~cm} / \mathrm{min}\) during both feed and purge steps. Use Eq. (20-15c) for solute velocities. Assume that wall heat capacities can be ignored, heat of adsorption is negligible, and no adsorption of n-heptane. Use solute movement theory to

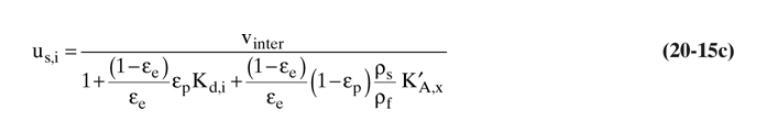
a. At what time does thermal wave exit (ignore wall effects)?

b. Predict the outlet concentrations of toluene versus time.

Us.i Vinter (1-e) & (1-E) (1-ep) Px KAx 1+di+ Ee Ee Pf (20-15c)