A continuous, steady-state distillation column is fed a mixture that is 70 \(\mathrm{mol} \% \mathrm{n}\)-pentane and \(30 \mathrm{~mol} \% \mathrm{n}\)-hexane. Feed rate is \(1000 \mathrm{kmol} / \mathrm{h}\). Feed is at \(35^{\circ} \mathrm{C}\). Column is at \(101.3 \mathrm{kPa}\). The vapor distillate product is \(99.9 \mathrm{~mol} \%\) \(\mathrm{n}\)-pentane, and the bottoms product is \(99.9 \mathrm{~mol} \% \mathrm{n}\)-hexane. The system has a partial condenser (thus, the distillate product is a saturated vapor) and operates at an external reflux ratio of \(\mathrm{L} / \mathrm{D}=2.8\). The reboiler is a partial reboiler. Find D, B, \(Q_{c}\), and \(Q_{R}\). Data are given in Problem 3.D6 and Table 2-7. Use the DePriester chart to determine boiling points.

Problem 3.D6

A distillation column receives a feed that is \(40 \mathrm{~mol} \% \mathrm{n}-\mathrm{pentane}\) and 60 \(\mathrm{mol} \% \mathrm{n}\)-hexane. Feed flow rate is \(2500 \mathrm{lbmol} / \mathrm{h}\), and feed temperature is \(30^{\circ} \mathrm{C}\). The column is at \(1 \mathrm{~atm}\). A distillate that is \(99.9 \mathrm{~mol} \%\) n-pentane is desired. A total condenser is used. Reflux is a saturated liquid. The external reflux ratio is \(\mathrm{L}_{0} / \mathrm{D}=3\). Bottoms from the partial reboiler is \(99.8 \mathrm{~mol} \% \mathrm{n}\) hexane. Find D, B, \(\mathrm{Q}_{\mathrm{R}}\), and \(\mathrm{Q}_{\mathrm{c}}\). Note: Watch your units on temperature.
\[
\begin{array}{ll}
\text { Data: } \lambda_{\mathrm{c} 5} & =11,369 \mathrm{Btu} / \mathrm{lbmol} \\
\lambda_{\mathrm{c} 6} & =13,572 \mathrm{Btu} / \mathrm{lbmol}, \text { both } \lambda \text { at boiling points. } \\
\mathrm{C}_{\mathrm{PL}, \mathrm{C} 5} & =39.7 \text { (assume constant) } \\
\mathrm{C}_{\mathrm{PL}, \mathrm{C} 6} & =51.7 \text { (assume constant) } \\
\mathrm{C}_{\mathrm{PV}, \mathrm{C}} & =27.45+0.08148 \mathrm{~T}-4.538 \times 10^{-5} \mathrm{~T}^{2}+10.1 \times 10^{-9} \mathrm{~T}^{3} \\
\mathrm{C}_{\mathrm{PV}, \mathrm{C6}} & =32.85+0.09763 \mathrm{~T}-5.716 \times 10^{-5} \mathrm{~T}^{2}+13.78 \times 10^{-9} \mathrm{~T}^{3}
\end{array}
\]
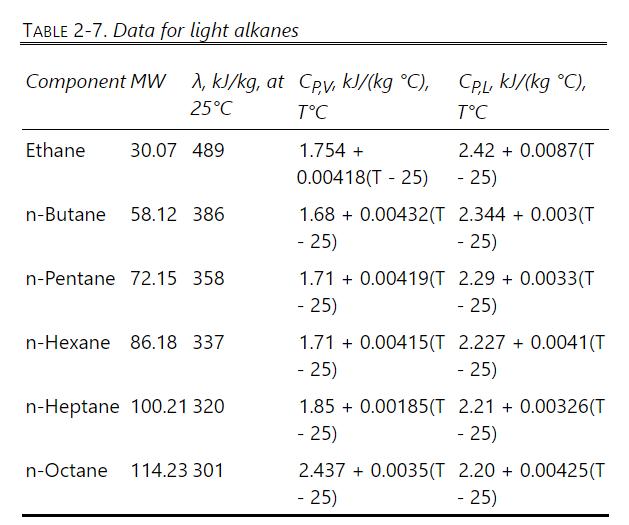
where \(\mathrm{T}\) is in \({ }^{\circ} \mathrm{C}\) and \(\mathrm{C}_{\mathrm{PV}}\) and \(\mathrm{C}_{\mathrm{PL}}\) are \(\mathrm{cal} /\left(\mathrm{mol}^{\circ} \mathrm{C}\right)\) or \(\mathrm{Btu} /\left(\mathrm{lbmol}{ }^{\circ} \mathrm{F}\right)\). Assume the heat of mixing is zero. Additional data are in Table 2-7. Source for \(\lambda\) and \(C_{P}\) data is Felder et al. (2018).

A distillation column receives a feed that is \(40 \mathrm{~mol} \% \mathrm{n}-\mathrm{pentane}\) and 60 \(\mathrm{mol} \% \mathrm{n}\)-hexane. Feed flow rate is \(2500 \mathrm{lbmol} / \mathrm{h}\), and feed temperature is \(30^{\circ} \mathrm{C}\). The column is at \(1 \mathrm{~atm}\). A distillate that is \(99.9 \mathrm{~mol} \%\) n-pentane is desired. A total condenser is used. Reflux is a saturated liquid. The external reflux ratio is \(\mathrm{L}_{0} / \mathrm{D}=3\). Bottoms from the partial reboiler is \(99.8 \mathrm{~mol} \% \mathrm{n}\) hexane. Find D, B, \(\mathrm{Q}_{\mathrm{R}}\), and \(\mathrm{Q}_{\mathrm{c}}\). Note: Watch your units on temperature.
\[
\begin{array}{ll}
\text { Data: } \lambda_{\mathrm{c} 5} & =11,369 \mathrm{Btu} / \mathrm{lbmol} \\
\lambda_{\mathrm{c} 6} & =13,572 \mathrm{Btu} / \mathrm{lbmol}, \text { both } \lambda \text { at boiling points. } \\
\mathrm{C}_{\mathrm{PL}, \mathrm{C} 5} & =39.7 \text { (assume constant) } \\
\mathrm{C}_{\mathrm{PL}, \mathrm{C} 6} & =51.7 \text { (assume constant) } \\
\mathrm{C}_{\mathrm{PV}, \mathrm{C}} & =27.45+0.08148 \mathrm{~T}-4.538 \times 10^{-5} \mathrm{~T}^{2}+10.1 \times 10^{-9} \mathrm{~T}^{3} \\
\mathrm{C}_{\mathrm{PV}, \mathrm{C6}} & =32.85+0.09763 \mathrm{~T}-5.716 \times 10^{-5} \mathrm{~T}^{2}+13.78 \times 10^{-9} \mathrm{~T}^{3}
\end{array}
\]
where \(\mathrm{T}\) is in \({ }^{\circ} \mathrm{C}\) and \(\mathrm{C}_{\mathrm{PV}}\) and \(\mathrm{C}_{\mathrm{PL}}\) are \(\mathrm{cal} /\left(\mathrm{mol}^{\circ} \mathrm{C}\right)\) or \(\mathrm{Btu} /\left(\mathrm{lbmol}{ }^{\circ} \mathrm{F}\right)\). Assume the heat of mixing is zero. Additional data are in Table 2-7. Source for \(\lambda\) and \(C_{P}\) data is Felder et al. (2018).

TABLE 2-7. Data for light alkanes Component MW , kJ/kg, at Cpv, kJ/(kg C), 25C CP,L, KJ/(kg C), TC TC Ethane 30.07 489 1.754 + 2.42+0.0087(T 0.00418(T - 25) - 25) n-Butane 58.12 386 1.68 0.00432(T 2.344 + 0.003(T -25) - 25) n-Pentane 72.15 358 1.71 0.00419(T 2.29 +0.0033(T -25) - 25) n-Hexane 86.18 337 1.71 -25) 0.00415(T 2.227 +0.0041(T -25) n-Heptane 100.21 320 1.85 -25) 0.00185(T 2.21 +0.00326(T - 25) n-Octane 114.23 301 2.437 +0.0035(T 2.20 + 0.00425(T - 25) -25)