A distillation column operating at \(200 \mathrm{kPa}\) separates \(100 \mathrm{kmol} / \mathrm{h}\) of a saturated liquid feed at \(200 \mathrm{kPa}\) that is \(20 \mathrm{~mol} \%\) propane (Pro), 35 \(\mathrm{mol} \% \mathrm{n}\)-pentane (Pen), and \(45 \mathrm{~mol} \% \mathrm{n}\)-hexane (Hex). The column has a total condenser and a partial reboiler. We want a fractional recovery of Hex in the bottoms \(=0.983\), and a fractional recovery of Pen in the distillate of 0.967 .

a. Make an appropriate assumption and determine flow rates of bottoms, \(\mathrm{B}\), and of distillate, \(\mathrm{D}\), in \(\mathrm{kmol} / \mathrm{h}\); and determine mole fractions of bottoms and of distillate.

b. Determine bubble-point temperature of feed and calculate relative volatilities at this temperature. Use Pen as your reference component. Report bubble-point temperature, \(\mathrm{K}\) values, and values of relative volatilities. Use DePriester charts or Eq. (2-28). Show your work.

Equation (2-28)

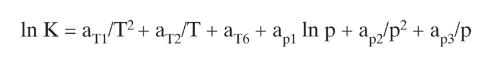
c. Assume relative volatilities found in part \(\mathrm{b}\) are constant, and determine minimum number of stages, \(\mathrm{N}_{\min }\), required for this separation.

d. Do a calculation that shows assumption made in part a is correct.

In K = a/T + a/T + a + a In p + a2/p + ap: pl +ap3/p