A gas-processing plant has an absorber and a stripper set up as shown in Figure \(12-2\), except both columns operate at \(25.0^{\circ} \mathrm{C}\) but are at different pressures. Absorber is at \(5.0 \mathrm{~atm}\) and stripper is at \(0.2 \mathrm{~atm}\). Feed to the plant is \(\mathrm{V}_{\mathrm{abs}}=100.0 \mathrm{kmol} / \mathrm{h}\) of air containing \(\mathrm{y}_{\mathrm{in}, \mathrm{abs}}=\mathrm{y}_{\mathrm{N}+1, \mathrm{abs}}=0.00098\) mole fraction 1,2,3-trichloropropane. Outlet gas from absorber is \(\mathrm{y}_{\mathrm{out}, \mathrm{abs}}=\mathrm{y}_{1, \mathrm{abs}}=\) 0.000079 mole fraction 1,2,3-trichloropropane. Inlet liquid to absorber is \(\mathrm{x}_{\mathrm{in}, \mathrm{abs}}=\mathrm{x}_{0, \mathrm{abs}}=0.00001\) mole fraction 1,2,3-trichloropropane. Note that because absorber and stripper are connected, \(\mathrm{x}_{\text {in,abs }}=\mathrm{x}_{\text {out,stripper }}\) and \(\mathrm{x}_{\text {out,abs }}=\) \(\mathrm{x}_{\text {in,stripper }}\). Entering gas in stripper is pure air. Determine the minimum liquid flow rate in the absorber and then operate with \(\mathrm{L}_{\mathrm{abs}}=1.6\left(\mathrm{~L}_{\mathrm{abs}, \mathrm{min}}\right)\). Note that \(\mathrm{L}_{\mathrm{abs}}=\mathrm{L}_{\text {stripper }}\) In the stripper determine the minimum gas flow rate, and operate with \(\mathrm{V}_{\text {stripper }}=1.5\left(\mathrm{~V}_{\text {stripper,min }}\right)\). Equilibrium data are in Table 12-2.

Figure 12-2

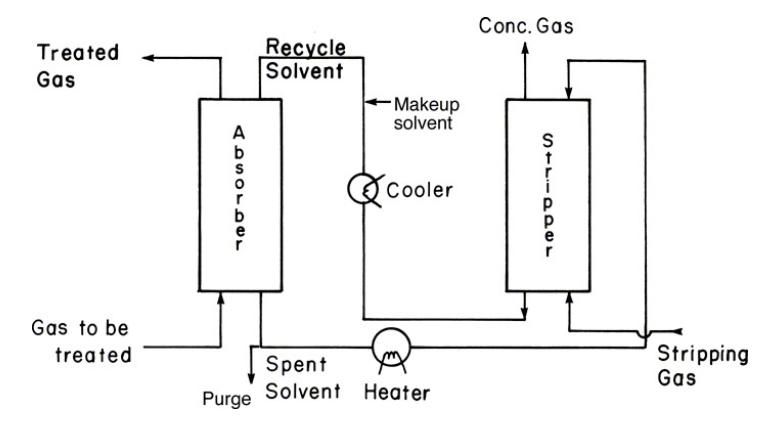
Table 12-2

a. Find \(\mathrm{L}_{\text {abs,min }}, \mathrm{L}_{\text {abs }}, \mathrm{x}_{\text {out,abs }}, \mathrm{N}_{\text {abs }}, \mathrm{V}_{\text {stripper,min }}, \mathrm{V}_{\text {stripper }}, \mathrm{y}_{\text {out,stripper }}\), and \(\mathrm{N}_{\text {stripper }}\)

b. Do mole fractions in the liquid ever exceed solubility limits?
Suggestion: Easiest solution path is to roughly sketch McCabe-Thiele diagrams to help in calculation of \(\mathrm{L}_{\text {abs,min }}\) and \(\mathrm{V}_{\text {stripper,min }}\), use external balances to find \(\mathrm{x}_{\text {out,abs }}=\mathrm{x}_{\text {in,stripper }}\) and \(\mathrm{y}_{\text {out,stripper }}\), and use the Kremser equation to find \(\mathrm{N}_{\text {abs }}\) and \(\mathrm{N}_{\text {stripper }}\) Watch your decimal points!

Transcribed Image Text:

Treated Gas Gas to be treated Conc. Gas Recycle Solvent Makeup solvent A b ADSOFDRL b Cooler STLIPPEL t Spent Solvent Heater Purge Stripping Gas