A more general scenario for the lubrication approximation is the problem where the fluid is contained in a gap of height \(h\), which is assumed to be a general function of \(x\), i.e., \(h=h(x)\).

The lower surface is assumed flat and moves with a velocity \(v\). The top surface can also move in the \(y\)-direction, and hence the gap height is changing at a rate of \(d h / d t\). This is similar to the squeezing flow in the previous problem. The velocity profile locally is the superposition of the Poiseuille flow and the Couette flow:

\[v_{x}=\frac{1}{2 \mu}\left(y^{2}-h y\right) \frac{d p}{d x}+V\left(1-\frac{y}{h}\right)\]

Develop an expression for the pressure distribution in the system using the lubrication approximation. For this the continuity equation is to be used in an integral sense rather than in a differential form:

\[\int_{0}^{h(x)}\left[\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{y}}{\partial y}\right] d y=0\]
The final equation turns out to be \[\frac{\partial h}{\partial t}=\frac{1}{\mu} \frac{\partial}{\partial x}\left(\frac{h^{3}}{12} \frac{\partial p}{\partial x}-\frac{v}{2} \frac{\partial h}{\partial x}\right)\]
Your task is to verify this. The above equation can then be used for a wide range of problems.

Previous problem:

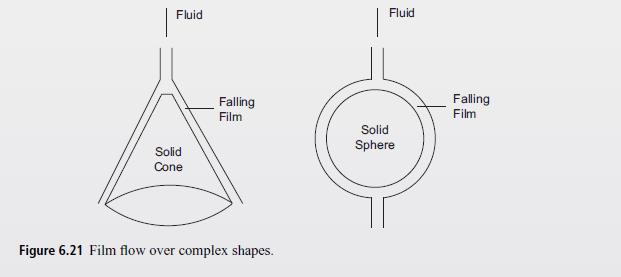
Consider the flow over a cone as shown in Fig. 6.21. Find the film thickness as a function of distance along the surface of the cone. Use the lubrication approximation. Repeat for the solid sphere in Fig. 6.21.

Transcribed Image Text:

Fluid Fluid Solid Cone Falling Film Figure 6.21 Film flow over complex shapes. Solid Sphere Falling Film