Numerical instability of forms of the Kremser equation used to calculate (mathrm{N}) can cause problems. Show that
Question:
Numerical instability of forms of the Kremser equation used to calculate \(\mathrm{N}\) can cause problems. Show that equations to calculate \(\mathrm{N}\) may have no answer because they would need to calculate the \(\ln\) (negative number) for large values of \(\mathrm{N}(\mathrm{N}>20)\) for the small and large values of \(\mathrm{L} /(\mathrm{mV})\) listed below. With \(\mathrm{L} /(\mathrm{mV})\) values given in part a or part \(\mathrm{b}\) do calculations for the following problem: \(\mathrm{x}_{1}=0, \mathrm{y}_{1}{ }^{*}=0, \mathrm{y}_{\mathrm{N}+1}=0.005\), and specified values of \(\mathrm{N}\).
a. \(\mathrm{L} /(\mathrm{mV})\) is small (use 0.22 ). Start with \(\mathrm{N}=21\) and first use Eq. (12-21) to determine \(\mathrm{y}_{\mathrm{N}+1} / \mathrm{y}_{1}\) and then use this value of \(\mathrm{y}_{\mathrm{N}+1} / \mathrm{y}_{1}\) to try Eq. (12-22) to calculate \(\mathrm{N}\). If it works, you expect to get the same value of \(\mathrm{N}\) back, but if the equation is close to failing, \(\mathrm{N}\) will not be exact. Increase \(\mathrm{N}\) and repeat the procedure until Eq. (12-22) does not work.
Equation (12-21)
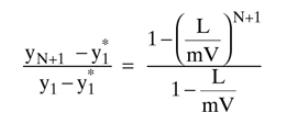
Equation (12-22)

b. \(\mathrm{L} /(\mathrm{mV})\) is large (use \(1 / 0.22)\). Start with \(\mathrm{N}=21\) and first use Eq. (12-31) inverted to determine \(\left(\mathrm{x}_{\mathrm{N}}-\mathrm{x}_{\mathrm{N}}{ }^{*}\right) /\left(\mathrm{x}_{0}-\mathrm{x}_{\mathrm{N}}{ }^{*}\right)\) and then use this value of \(\left(\mathrm{x}_{\mathrm{N}}\right.\) \(\left.-\mathrm{x}_{\mathrm{N}} *\right) /\left(\mathrm{x}_{0}-\mathrm{x}_{\mathrm{N}}{ }^{*}\right)\) to try Eq. (12-28) to calculate \(\mathrm{N}\). Increase \(\mathrm{N}\) and repeat the procedure until Eq. (12-28) does not work.
Equation (12-28)
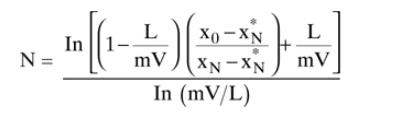
c. Of course, in a design problem, \(\mathrm{N}\) will be unknown and either \(\mathrm{y}_{\mathrm{N}+1}\) or \(\mathrm{x}_{\mathrm{N}}\) will be specified. What can you do if \(\mathrm{L} /(\mathrm{mV})\) is small, \(\mathrm{y}_{\mathrm{N}+1}\) is specified, and your attempt to calculate \(\mathrm{N}\) from Eq. (12-22) fails?
Equation (12-22)

Step by Step Answer:

Separation Process Engineering Includes Mass Transfer Analysis
ISBN: 9780137468041
5th Edition
Authors: Phillip Wankat





